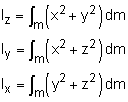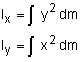| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Moment of Inertia | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
Mass is a measure of a body's resistance to linear acceleration, F = ma Similarly, moment of inertia is a measure of a body's resistance to angular acceleration,
The moment of inertia Io is defined as the integral of the "second moment" about an axis Lo of all the elements of mass dm that compose the body: Here, r is the perpendicular distance from the axis Lo to an element dm. The value of Io depends on the shape of the body and the location of the axis about which Io is calculated. If the axis passes through the center of gravity, then the axis is denoted L, and the moment of inertia is denoted I. The moment of inertia for each coordinate axis can also be transformed as
|
||||
| Thin Plates with Uniform Thickness |
|||||
 Moment of Inertia for Thin Objects with Uniform Thickness |
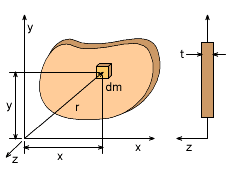
For thin objects with uniform thickness in the z-direction (2-D problems), the axis of rotation is perpendicular to the x-y plane, the mass moment of inertia equation be written as Notice, the z2 term was dropped since it is a thin plate. Similarly, the moment of inertia about the x- and y-axis for a thin object with uniform thickness, can be express as Since the plate is thin, the moment of inertia about the z-axis can be written as This form is easier to use if Ix and Iy are known and is particularly helpful if you have access to tables giving the area moment of inertia (see Sections Appendix). See below how to convert the 'area moment of inertia' to the 'mass moment of inertia' for thin plates. |
||||
| Objects with Multiple Parts |
|||||
 Moment of Inertia for point mass objects in the x-y plane |
The moment of inertia of a complex object can be determined by summing the moments of inertia of its individual parts. This is useful if the individual parts of a complex object can be analyzed as simple objects. This concept can be summarize in equation form as where the i subscript represents each individual objects. |
||||
| Parallel Axis Theorem |
|||||
|
|
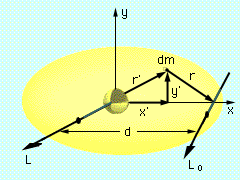
If the moment of inertia I about an axis L passing through an object's center of gravity is known, then the moment of inertia about any other parallel axis Lo can be determined. Consider the object shown at the left, The parallel axis theorem assumes that the moment of inertia is moving from the center of gravity (usually the centroid) to a new location. The theorem cannot be used to move the moment of inertia from an arbitrary point to another arbitrary point. One of the the two points must be the center of gravity. |
||||
| Comparison of Area I and Mass I |
|||||
The moment of inertia used in Dynamics is Mass Moment of Inertia and has units of length2 - mass. This is different from the moment of inertia used in Statics and Mechanics of Material courses, called the Area Moment of Inertia, which has units of length4. It is important not to mix these two since they are different but related. For a thin plate, the mass and area moment of inertia are related as Imass = Iarea t ρ where t is the plate thickness and ρ is the homogenous density of the plate. |
|||||
| Radius of Gyration of a Mass |
|||||
 Radius of Gyration of a Mass Iaxis = mk2 |
The radius of gyration of a mass, k, is sometimes used to define the moment of inertia for odd shaped objects. For a body of mass m, the moment of inertia about a given axis is Iaxis = mk2 The radius of gyration is not calculated for odd shaped objects, but must be given or determined from experimental results. The radius of gyration is commonly to tabulate the moment of inertia of unsymmetrical sections in handbooks. |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.