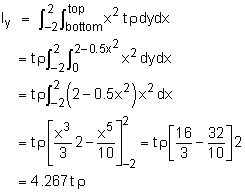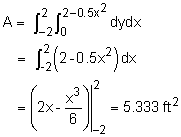| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Moment of Inertia | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Thin Plate |
Example |
|
|
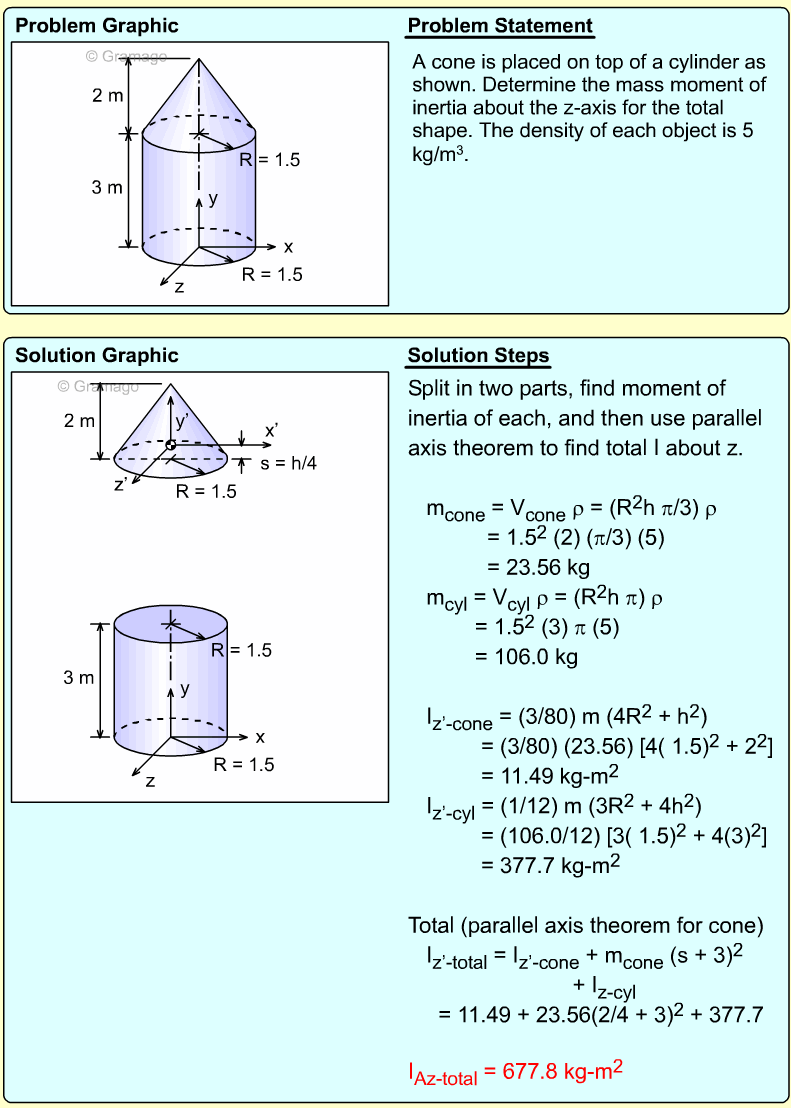
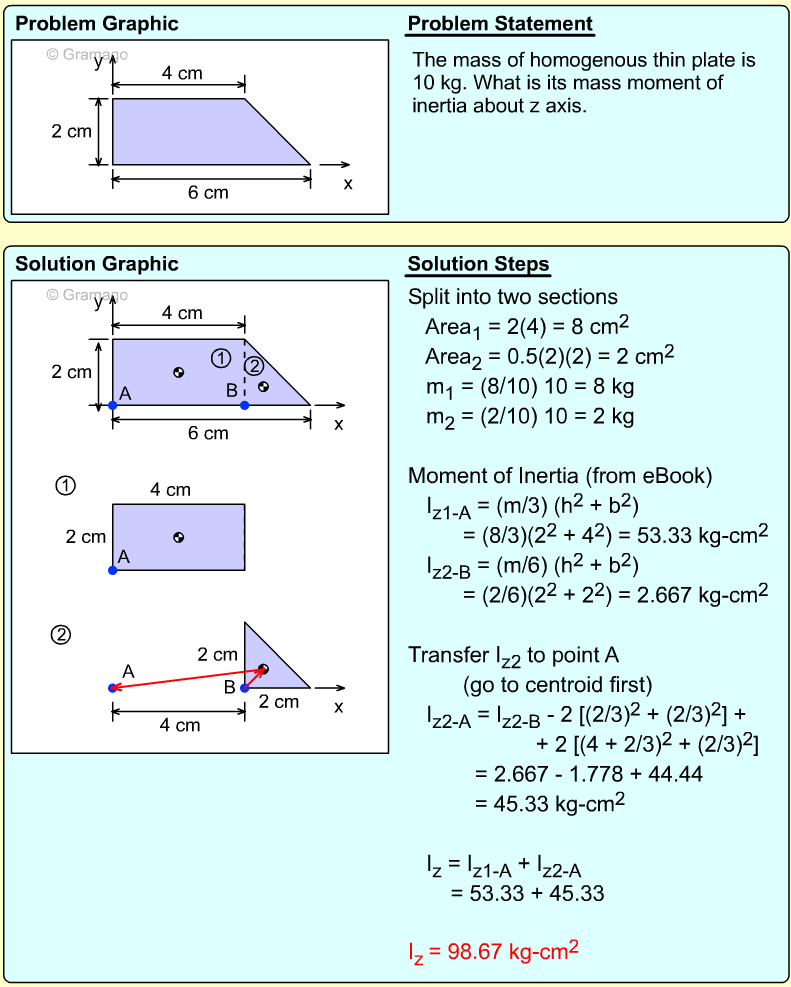
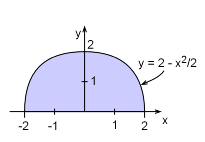
A homogeneous thin plate with uniform thickness weighs 20 lb. What is its mass moment of inertia about Y axis? Note, the shape is not a semi-circle. Assume all dimensions are in feet. |
||
| Solution |
||
|
|
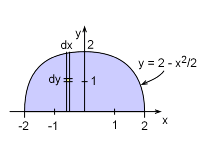
The mass moment of inertia about the y-axis for a uniform plate is defined as where the dm is the mass of an infinitesimal volume. However, dm can be converted into x and y dimensions using t as the plate thickness and ρ as the mass density, or |
|
 Integration Section |
The limits of integration are -2 to 2 for x, and the plate bottom to the plate top for y. This gives, The density of the plate is simply, The moment inertia becomes, To find the plate area, just integrate as The final moment of inertia is |
|
| Example Problem 1 |
||
|
||
| Example Problem 2 |
||
|
||
| Example Problem 3 |
||
|
||
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||
| Example Problem 10 |
||
|
||
| Example Problem 11 |
||
|
||
| Example Problem 12 |
||
|
||
| Example Problem 13 |
||
|
||
| Example Problem 14 |
||
|
||
| Example Problem 15 |
||
|
||
| Example Problem 16 |
||
|
||
| Example Problem 17 |
||
|
||
| Example Problem 18 |
||
|
||
| Example Problem 19 |
||
|
||
| Example Problem 20 |
||
|
||