Deflection of a Cantilever Beam

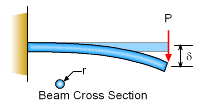
Step 1: In the study of the deflection of a cantilever beam, the parameters involved are the applied force (P), deflection (δ), modulus of elasticity (E), beam radius (r) and beam length (l). A total of 5 parameters (n = 5) is involved in this problem.

Step 2: The basic dimensions involved are summarized in the following table

Hence, 2 basic dimensions (k = 2) are involved in this problem.

Step 3: According to the Buckingham pi theorem, the number of pi terms is 3 (n - k = 5 - 2 = 3).

Step 4: The next task is to determine the form of the pi terms. Select the modulus of elasticity (E) and beam radius (r) as the repeating parameters.

The pi terms are then given by:

     Π₁ = PE^a1r^b1
     Π₂ = δE^a2r^b2
     Π₃ = lE^a3r^b3

The exponents of the first pi terms are determined as follows:

     Π₁ = PE^a1r^b1 = (F)(FL^-2)^a1(L)^b1
             = F^{(1 + a1)} L^{(-2a1 + b1)}

In order for Π₁ to be dimensionless:

     F:     1 + a1 = 0
              a1 = -1

     L:     -2a1 + b1 = 0
             b1 = 2(-1) = -2

Hence, Π₁ is determined to be P/Er².

By inspection, the second and third pi terms are given by (a2 = 0, b2 = -1, a3 = 0 and b3 = -1):

      Π₂ = δ/r     
      Π₃ = l/r

Hence according to the dimensional analysis, the important parameters are

     δ/r = function(P/Er², l/r)

Note: According to the beam bending theory, the deflection of a circular beam is given by

     

Recast the above equation in terms of the dimensionless parameters to yield

     

which is in agreement with the results obtained from dimensional analysis.