| Ch 6. Rigid Body Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Moment of Inertia |
Translational Motion | Fixed Point Rotation |
General Plane Motion |
||||
| Moment of Inertia | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
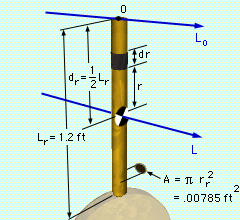 Dimensions |
First find the moment of inertia of the slender rod about a line L passing through its center of mass. "Slender" means the length is much greater than the width or depth. Consider a differential element of length dr at a distance r from the center of mass. The mass of the element is equal to the product of its density and volume: dm = ρ dv = ρ A dr Substitute this into equation for the moment of inertia of the rod about L, Note that the mass of the rod is given by mr = ρ Vrod = ρ A Lr thus Irod = 1/12 mr Lr2 This is the same result listed in the Sections Appendix. for a slender rod. |
|
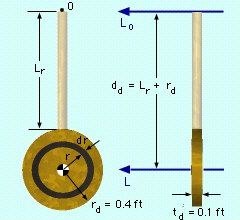 Dimensions |
Now the parallel axis theorem can be used to calculate the moment of inertia of the rod about the line Lo passing through the point 0, Io-rod = Irod + dr2 mr = 1/12 mr Lr2 + (1/2 Lr)2 mr = 1/3 mr Lr2 = 0.3333 (0.5 slugs) (1.2 ft)2 = 0.2400 slugs-ft2 Next, determine the moment of inertia of the disk about a line L passing through its center of mass, perpendicular to the flat face of the disk. Consider a differential element of width dr at a radius r from the center of mass. The mass of the element is equal to the product of its density and volume: dm = ρ dv = ρ td 2 π r dr Substitute this into the moment of inertia equation to get I of the disk about L, = 0.5 ρ td π rd4 The mass of the element is equal to the product of its density and volume, md = ρ Vd = ρ π rd2 td Idisk = 1/2 md rd2 Again, parallel axis theorem can be used to find the moment of inertia of the disk about the line Lo passing through the point 0, Io-disk = Idisk + dd2 md = 1/2 md rd2 + (Lr + rd)2 md = md [1/2 rd2 + (Lr + rd)2] = 2.67 [1/2 (0.4)2 + (1.2 + 0.4)2] = 7.049 slugs-ft2 |
|
The sum of the moment of inertia of the disk and rod to will give the total moment of inertia of the pendulum about Lo as Io-pendulum = Io-rod + Io-disk = 7.289 slugs-ft2 |
||