| Ch 5. Second Law of Thermodynamics | Multimedia Engineering Thermodynamics | ||||||
| Heat Engine |
The Second Law |
Carnot Cycle |
Carnot Heat Engine |
Carnot Refrigerator |
|||
| Carnot Heat Engine | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||||||
| The Thermodynamic Temperature
Scale
|
|
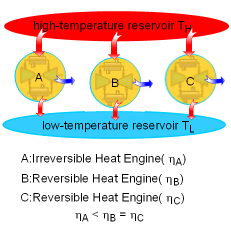
A temperature scale which is independent of the properties of the substances that are used to measure temperature is called a thermodynamic temperature scale. Its derivation is given below using some Carnot heat engines. The Carnot principle states that the reversible heat engines have the highest efficiencies when compared to irreversible heat engines working between the same two reservoirs. And the efficiencies of all reversible heat engines are the same if they work between the same two reservoirs. That is, the efficiency of a reversible heat engine is independent on the working fluid used and its properties, the way the cycle operates, and the type of the heat engine. The efficiency of a reversible heat engine is a function of the reservoirs' temperature only. ηth = 1 - QL/QH = g(TH,TL) or QH/QL = f(TH,TL) where |
|||||||
|
|
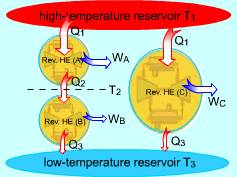
Consider three reversible heat engines working between a high-temperature reservoir at temperature T1 and a low-temperature reservoir at temperature T3. Engine A receives Q1 from the high-temperature reservoir,and rejects Q2 to engine B at temperature T2. Engine B receives Q2 from engine A at temperature T2, and rejects Q3 to the low-temperature reservoir. Engine C receives Q1 from the high-temperature reservoir,and rejects Q3 to the low-temperature reservoir. Applying the equation above to the three engines separately yields, Engine A: Q1/Q2 = f(T1,T2)
(1) Multiplying equations (1) and (2) gives Comparing (4) and (3) yields, f(T1,T3) = f(T1,T2)f(T2,T3) 5) The left-hand side of equation (5) is only a function of T1 and T3, and thus the right-hand side of equation (5) is also a function of T1 and T3 only. This condition will be satisfied only if the function f has the following form: Substituting them to equation (5) gives, or, Equation (6) provides a basis to define a thermodynamic temperature scale. There are several choices for the function φ. The Kelvin scale is obtained by making a simple choice as φ(T) = T Hence, equation (6) becomes, Q1/Q3 = T1/T3 To bring uniformity to the treatment of heat engines, H is used to denote the high-temperature reservoir, and L to denote the low-temperature reservoir. The above equation becomes, QH/QL = TH/TL |
||||||||
|
|
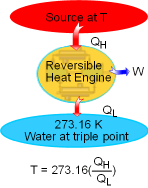
The Kelvin scale temperature is called absolute temperature. At the International Conference on Weights and Measures held in 1954, the triple-point of water was assigned the value 273.16 K. Then, if a reversible cycle is operated between a reservoir at 273.16 K and another reservoir at temperature T, temperature T can be expressed as T = 273.16(Q/Qtp)rev. cycle where Q and Qtp are heat transfer between the cycle and the reservoirs at temperature T and at temperature 273.16 K, respectively. The magnitude of a Kevin scale is defined as 1/273.16 of the temperature interval between the absolute zero and the tripe-point of water. The magnitude of temperature units on Kevin scale is the same as that of Celsius. 1 K When numerical values of the thermodynamic temperature are to be determined,
it is not possible to use a reversible cycle since that does not exist
in practice. Absolute temperatures can be measured by other means,
such as the constant-volume ideal gas thermometer. |
||||||||
| The Carnot Heat Engine
|
|||||||||
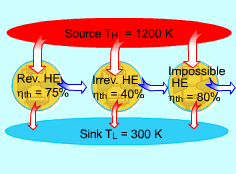 A Carnot Heat Engine has the Highest Efficiency of any Heat Engines Working between the Same Source and Sink |
A heat engine is called a Carnot heat engine if it operates on the reversible Carnot cycle. The thermal efficiency of heat engine, regardless reversible or irreversible, is given as ηth = 1- QL/QH where QL and QH are heat transfer between the cycle and the low-temperature reservoir at temperature TL and the high-temperature reservoir at temperature TH, respectively. For reversible heat engines, the heat transfer ratio can be replaced by the absolute temperatures of the two reservoirs. ηth = 1- TL/TH This efficiency is called the Carnot efficiency since the Carnot heat engine is one of the well-known reversible engines. It is the highest efficiency that a heat engine working between a high-temperature reservoir at temperature TH and a low-temperature reservoir at temperature TL can reach. All irreversible heat engines working between the same two reservoirs have lower efficiencies.
|
||||||||
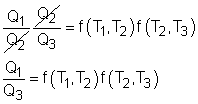 (4)
(4)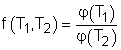 and
and 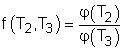
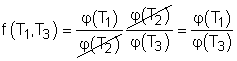
 (6)
(6)