| Ch 5. Rigid Body Equilibrium | Multimedia Engineering Statics | ||||||
|
2-D and 3-D Supports |
Equilibrium in 2-D |
Equilibrium in 3-D |
Indeterminate Objects | 2 and 3 Force Members | |||
| Indeterminate Objects | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
With a statically indeterminate object, the reactions exerted on the object by its supports cannot be found using only the equilibrium equations. There are two types of static indeterminacy. |
||
| Type 1: Redundant Supports |
||
|
|
If the supports of a rigid body exert more unknown reactions than the maximum number of equilibrium equations available, then the system is statically indeterminate, and additional equations will be required to determine the reactions. This occurs when a rigid body has more restraints than the minimum number necessary to maintain equilibrium; the supports are said to be redundant. The difference between the number of reactions and the number of equilibrium equations is called the degree of redundancy. |
|
|
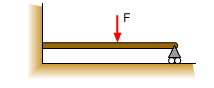
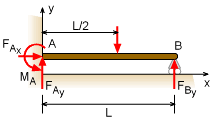
As an example of a rigid body under the action of a 2-D system of redundant supports, consider a horizontal beam that is fixed at one end and supported by a roller at the other end as illustrated in the diagrams to the left. There are four unknown reactions, FAx FAy MA FBy However, there are only three independent equilibrium equations, ΣFx = FAx = 0 ΣFy = FAy + FBy - F = 0 ΣMA = MA - 1/2 LF + LFBy = 0 The horizontal beam in the previous diagram has a degree of redundancy of one. With only three equilibrium equations, all four unknowns cannot be determined. In some cases, however, some of the reactions can be determined by using the equilibrium equations. In this case, for example, the first equation indicates that FAx = 0. Systems such as this one can be solved by supplementing the equilibrium equations with additional equations that relate the reactions to the deformation of the rigid body. This is the subject of Mechanics of Materials. |
|
| Type 2: Improper Supports |
||
|
If the supports of a rigid body are unable to maintain equilibrium under the applied loads, then the rigid body will move, and the system is improperly supported or unstable. There are two common scenarios that can lead to improper supports. |
||
 Parallel Reaction Forces |
||
| Parallel Reaction Forces |
||
|
If the supports exert only parallel reaction forces, then the rigid body is free to move in directions perpendicular to the reactions. Consider a horizontal beam supported by two rollers, If an external load is applied that has a horizontal component, there is no reaction force to prevent the beam from moving in the horizontal direction, and the beam has improper supports. |
||
| Concurrent Reaction Forces |
||
 Concurrent Reaction Forces |
If the supports exert only concurrent forces-that is, the lines of action of all the support forces intersect at one point-and the external loads produce a moment about the point of intersection, then the rigid body is not in equilibrium. Consider a horizontal beam supported by two rollers, each on an incline. The lines of action of the reaction forces of the rollers intersect. If an external load is applied that creates a moment about the point of intersection, then the beam will not be in equilibrium. Note that if the line of action of the external load intersects the same point as the reaction forces, there will be no moment about the point of intersection, and the beam will be in equilibrium. |
|