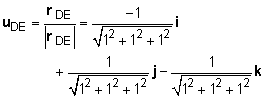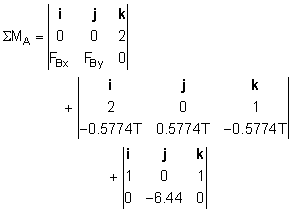Force Diagram

Position Vectors Diagram

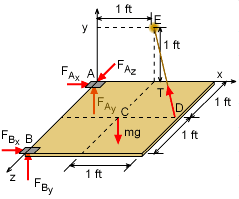
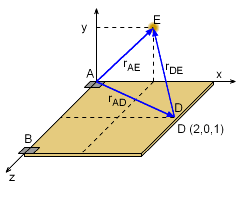
The process for analyzing a rigid body in equilibrium subject to a 3-D system of forces is similar to that of a 2-D system of forces. Begin by drawing a free-body diagram.

To use the equilibrium equations, the tension in the rope must be expressed in terms of its rectangular components. Using the coordinates of points D and E, the position vector from D to E is

     r_DE = r_AE - r_AD

           = (1i + 1j + 0k) - (2i + 0j + 1k)

     r_DE = -1i + 1j - 1k

Divide r_DE by its magnitude to get a unit vector that is parallel to the axis of the rope.

   u_DE = -0.5774i + 0.5774j - 0.5774k

Use this unit vector to express the tension in the rope in terms of rectangular components:

     T = T u_DE

        = T ( -0.5774i + 0.5774j - 0.5774k)

Using the equilibrium equations, sum the forces,

      ΣF_x = F_Ax + F_Bx - 0.5774 T = 0                       (1)
      ΣF_y = F_Ay + F_By + 0.5774 T
                       + (0.20 slug)(-32.2 ft/s²) = 0         (2)
      ΣF_z = F_Az - 0.5774 T = 0                                (3)

Next, sum the moments about point A. This will will give a vector equation representing moments around all three axis that go through A, x-axis, y-axis, and z-axis.

     ΣM_A = r_AB × F_B + r_AD × T
                  + r_AC x (0.20 slug)(-32.2 ft/s²)j = 0

     ΣM_A = (-2F_By - 0.5774 T + 6.44)i
                  + (2F_Bx + 0.5774 T)j 
                       + (1.1548T - 6.44)k

     ΣM_x = -2F_By - 0.5774 T + 6.44 = 0                  (4)
     ΣM_y = 2F_Bx + 0.5774 T = 0                             (5)
     ΣM_z = 1.1548T - 6.44 = 0                               (6)

Solving Eqs. 1-6 simultaneously gives the components of reaction in each support, and the tension in the rope.

     F_Ax = 4.830 lb
     F_Ay = 1.610 lb
     F_Az = 3.220 lb
     F_Bx = -1.610 lb
     F_By = 1.610 lb
     T = 5.577 lb