| Ch 5. Second Law of Thermodynamics | Multimedia Engineering Thermodynamics | ||||||
| Heat Engine |
The Second Law |
Carnot Cycle |
Carnot Heat Engine |
Carnot Refrigerator |
|||
| The Second Law | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||
|
|
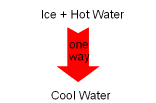
In nature, processes occur in a certain direction, and not in the reverse direction. For example, if a block of ice is put into a cup of hot water, the ice will melt and the temperature of the water will decrease as a result of heat transferred from the higher temperature water to the lower temperature ice. This process is satisfied the first law of thermodynamics, which requires the energy lost by the water equals the energy gained by the ice. Consider the reverse process. A block of ice is put into a cup of hot water. Heat is transferred from the ice to the water. As a result, the water temperature increases and the ice temperature decreases. This process still obeys the first law. That is, the energy lost by the block of ice equals the energy gained by the water. But this process never occurs. This example shows that if a process only satisfies the first
law, it may not occur. Hence, another law must also be obeyed
to guarantee a process
to happen. This is the second law of thermodynamics. A process will
not occur unless it satisfies both the first and the second laws
of thermodynamics. |
||
| Clausius Statement of the Second Law
|
|||
 Clausius Statement of the Second Law |
The Clausius statement of the second law states
Heat can transfer from a cooler body to a hotter body if other
effects accomplishing the heat transfer occur within the system or its
surroundings, or both. Air conditioners and refrigerators are devices
to transfer heat from a cool space to its hot surroundings. But
both of them need power input. The Clausius statement says that an air
conditioner cannot cool a room without power input. |
||
| Kelvin-Planck Statement of the Second Law |
|||
 Kelvin-Plank Statement of the Second Law |
A heat engine must reject some energy to a heat sink in order to run a cycle. That is, no heat engine can convert all the heat it received from a high-temperature source to work. It is the basis for the Kelvin-Planck statement of the second law of thermodynamics, which is
The Kelvin-Planck statement puts forward the idea that no heat engine can
have 100 percent efficiency. It must exchange heat with a low-temperature
heat sink as well as a high-temperature source to complete the thermodynamic
cycle. |
||
| Equivalence of Two Statement
|
|||
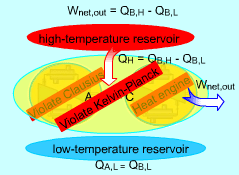
The Clausius statement and the Kelvin-Planck statement of the second law of thermodynamics are equivalent in their consequences. Any device that violates the Kelvin-Planck statement also violates the Clausius statement. |
|||
 Any Device that Violates the Kelvin-Plank Statement also Violates the Clausius Statement
|
Consider two devices A and B working between a high-temperature
reservoir and a low-temperature reservoir. Device A is assumed to transfer
Heat (QA,H) to work ( WA, net) and have
100 percent efficiency. That is, Device A violates the Kelvin-Planck statement. Device B is a heat pump which receives heat (QB,L) from the low-temperature reservoir, receives work (WA, net) from device A and rejects the total energy of WA, net and QB,L to the high-temperature reservoir. Heat rejected by device C, which is the combination of devices A and B, to the high-temperature reservoir equals (QB,L + WA,net)
- QA,H Device C receives heat (QB,L) from the low-temperature reservoir and rejects the same amount of heat (QB,L) to the high-temperature reservoir. It violates the Clausius statement. |
||
|
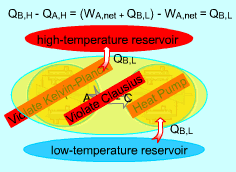
It can also be shown in a similar way that if a device violates the Clausius statement, it also violates the Kelvin-Planck statement. Hence, the Clausius statement and the Kelvin-Planck statement are two equivalent expressions of the second law of thermodynamics. |
||
| Perpetual-Motion Machines
|
|||
The previous discussion shows that a process will not occur unless it satisfies both the first and the second laws of thermodynamics. But before this was commonly understood, a lot of efforts were spent to create machines which violate the first law or the second law. This kind of machines are called perpetual-motion machines. Devices that violate the first law are called perpetual-motion machines of the first kind (PMM1). Devices that violate the second law are called perpetual-motion machines of the second kind (PMM2). |
|||