Ch 5. Rigid Body Equilibrium     Multimedia Engineering Statics
2-D and
3-D Supports		 Equilibrium
in 2-D		 Equilibrium
in 3-D		 Indeterminate Objects 2 and 3 Force Members      
Statics
 Equilibrium in 2-D Case Intro Theory Case Solution Example
 Chapter
 1. Basics
 2. Vectors
 3. Forces
 4. Moments
 5. Rigid Bodies
 6. Structures
 7. Centroids/Inertia
 8. Internal Loads
 9. Friction
 10. Work & Energy
 
 Appendix
 Basic Math
 Units
 Sections
 
 eBooks
 Dynamics
 Fluids
 Math
 Mechanics
 Statics
 Thermodynamics
 
©Kurt Gramoll
STATICS - EXAMPLE
    Example


Beam with Distributed Load

 

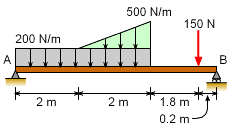
Calculate the reaction forces acting at A and B on the beam.

   
  Solution

 

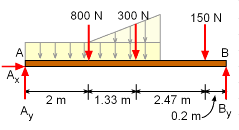
First convert the distributed loads into point loads and find their locations.

For a rectangular uniform distributed load, the magnitude of the resultant force will be the product of the length of the rectangle and value of the distributed load. The location of the force resultant is always the center point (centroid) of the distributed load. The magnitude of the resultant force will be

     (200 N/m) (4 m) = 800 N

and it will be at 2 m away from support A.

For a triangular line load, the force resultant is one half of the peak value of the distributed load multiplied by the distance over which it acts. The location of the force resultant is two-thirds of the distance from the vertex to the peak value of the load. The magnitude of the resultant force will be

     (1/2) (2) (500 - 200) = 300 N

and it is at 1.33 m from left vertex.

The actual reactions can be found by applying equilibrium equations

   
   

There will be three possible reactions at A and B namely Ax, Ay and By. which can be found by applying the equilibrium equations.

     ΣMA = 0
     By (6) - 800 (2) - 300 (3.33) - 150 (5.8) = 0
     By = 578.2 N

Equating forces give,

     ΣFy = 0
     Ay + By - 800 - 300 - 150 = 0
     Ay = 671.8 N

Since there is no horizontal applied load, Ax will be zero.

     
Example Problem 1
   

     
Example Problem 2
   

     
Example Problem 3
   

     
Example Problem 4
   

     
Example Problem 5
   

     
Example Problem 6
   

     
Example Problem 7
   

     
Example Problem 8
   

     
Example Problem 9
   

     
Example Problem 10
   

     
Example Problem 11
   

     
Example Problem 12
   

     
Example Problem 13
   

     
Example Problem 14
   

     
Example Problem 15
   

     
Example Problem 16
   

     
Example Problem 17
   

     
Example Problem 18
   

     
Example Problem 19
   

     
Example Problem 20
   

     
Example Problem 21
   

     
Example Problem 22
   

     
Example Problem 23
   

     
Example Problem 24
   

     
Example Problem 25
   

     
Example Problem 26
   

     
Example Problem 27
   

     
Example Problem 28
   

     
Example Problem 29
   

     
Example Problem 30
   

     
Example Problem 31
   

     
Example Problem 32
   

     
Example Problem 33
   

     
Example Problem 34
   

     
Example Problem 35
   

     
Example Problem 36
   

     
Example Problem 37
   

     
Example Problem 38
   

     
Example Problem 39
   

     
Example Problem 40
   

     
Example Problem 41
   

     
Example Problem 42
   

     
Example Problem 43
   

     
Example Problem 44
   

     
Example Problem 45
   

     
Example Problem 46
   

     
Example Problem 47
   

     
Example Problem 48
   

     
Example Problem 49
   

     
Example Problem 50
   

     
Example Problem 51
   

     
Example Problem 52
   

     
Example Problem 53
   

     
Example Problem 54