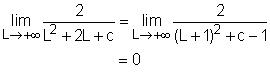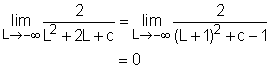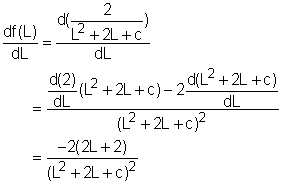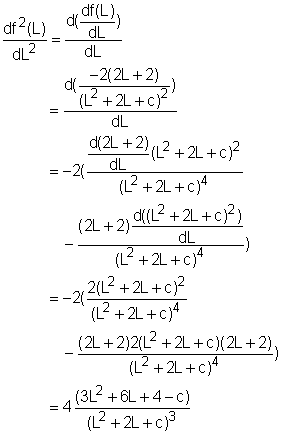| Ch 5. Curve Sketching | Multimedia Engineering Math | ||||||
|
Curve Sketching |
Graphing | ||||||
| Graphing | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
In this function, the independent variable is L, the dependent variable is f(L), and c is a integer larger than 0. This function is a family of curves with c as constant. One common feature is the function has the same horizontal asymtote. When L approaches -∞ or +∞the limit of the function is Similarly, So the curves for this family of functions have x axis as the horizontal asymptote. It is given that the value of c is an positive integer and the distance among atoms is larger than 0. This makes the value of L2 + 2L + c larger than 0, and thus, the curves do not have vertical asymptote. Setting L equals 0, the y intercept can be
found. In order to analyze the monotonicity of the function, the first derivative is calculated. That is According to this expression, when L is less than -1, the first derivative of the function is positive, and thus its curve is increasing. On the other hand, when L is larger than -1, the first derivative of the function is negative, and thus, its curve is decreasing. |
||
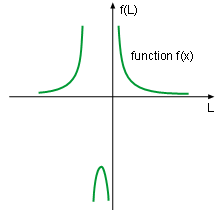 Function f(L) = 2/(L2 + 2L + 0) |
The critical points occurs when the first derivative equals 0, which is at -1. The local extreme value can be calculated at the critical points as f(-1) = 2/((-1)2 + 2(-1) + c) = 2/(c-1) It has been mentioned previously that when L > -1, the sign of the first derivative is negative, and when L < -1, the sign of the first derivative is positive. Therefore, the function has local maximum at point L = -1 and its value is 1/(c-1). The curve for this family of functions is shown in the diagrams at the left and below. |
|
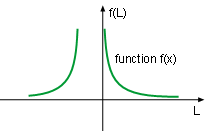 Function f(L) = 2/(L2 + 2L + 1) |
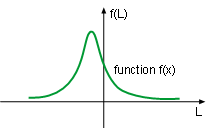 Function f(L) = 2/(L2 + 2L + 2) |
|
| Discussion |
||
Notice that in this problem, the extreme value are not calculated through the second derivative test. This is due, in part, to the complicated second derivative and does not help to find the sign of the function. The expression of the second derivative is given below. |
||
Another interesting issue is what the curve looks like if c is negative, such as -1 or -2. Sketch them with the simulation in this section and see the results. In this case study, L is the distance among atoms and must be positive. In the three diagrams, Function f(L) = 2/(L2 + 2L + 0), Function f(L) = 2/(L2 + 2L + 0), and Function f(L) = 2/(L2 + 2L + 0), the negative side of the diagram is plotted to show the full curves of this family function. |
||