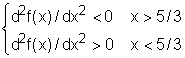| Ch 5. Curve Sketching | Multimedia Engineering Math | ||||||
|
Curve Sketching |
Graphing | ||||||
| Curve Sketching | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||||||||||||||||||||||
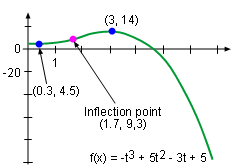
Sketch the curve of the function f(t) = -t3 + 5t2 - 3t + 5 and show all the significant features on it. |
|||||||||||||||||||||||||
It is given that the life cycle of Auxin is 7 weeks, so the domain of the function is (0, 7). Setting x equals 0, y intercept can be found. That is f(0) = 5 Setting f(x) = 0, x intercept can be calculated. That is -t3 + 5t2 - 3t + 5 = 0 Since this equation involves a high order polynomial function, it is hard to calculate. However, an estimated value of 5 weeks can be determined and used for preliminary plotting. Substituting -x into the function to determine the odevity of the cell elongation speed function and gives f(-x) = -(-t)3 + 5(-t)2 -
3(-t) + 5 Since f(-x) ≠ f(x) and f(-x) ≠ -f(x), this function is not symmetric with respect to origin or y axis. Next, calculate the first derivative to determine the monotonocity of the function. That is df(x)/dx = -3t2 + 10t - 3 The critical points occurs when the derivative equals 0, which is at 1/3 and 3. The domain of time is between 0 and 7, which is broken down to three intervals by 1/3 and 3, they are (0, 1/3), (1/3, 3), and (3, 7). The sign and the monotonicity are shown in the table. A "+" indicates a positive expression and a "-" means a negative expression. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
The local extreme values can be calculated at the critical points. They are f(1/3) = -(1/3)3 + 5(1/3)2 - 3(1/3) + 5 = 122/7 = 4.5 f(3) = -(3)3 + 5(3)2 - 3(3) + 5 = 14 Therefore, the local minimum value is 4.5 and the local maximum value is 14. |
|||||||||||||||||||||||||
 Remaining Distance Sequence |
In order to analyze the concavity and find the inflection point, the second derivative is needed. That is d2f(x)/dx2 = d(-3t2 + 10t - 3)/dx = -6t + 10 Thus, the inflection point is at ( 1.7, 9.3) Therefore, The curve is concave upward on (0, 5/3) and concave downward on (5/3, 7). According to all the information listed above, the curve of the function f(t) = -t3 + 5t2 - 3t + 5 is sketched on the left with all the significant features. |
||||||||||||||||||||||||