| Ch 5. Fundamental Laws (Differential) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Navier-Stokes and Euler's |
Conservation Energy |
|||||
| Conservation of Mass | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
|
|
The given steady two-dimensional velocity profile is where u = 3(x2 - y2) and v = -6xy. Since To this end, the flow field is known to be two-dimensional and incompressible, hence a stream function can be introduced. According to the definition of the stream function, The two equations above can be integrated to yield, ψ = 3x2y - y3 +
f1(x) |
|
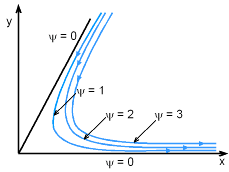 Streamlines |
In order for the stream function, ψ, to satisfy the two equations simultaneously, it must have the form ψ = 3x2y - y3 + C where C is an arbitrary constant. For simplicity, set C = 0 (recall, the value of an individual stream function is irrelevant) to yield, ψ = 3x2y - y3 Streamlines can now be drawn by setting the stream function to a constant. For instance, the plots of ψ = 0, 1 and 2 are shown in the figure. Note that ψ = 0 in this case corresponds to the wall. |
|