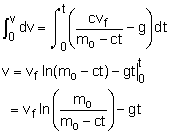| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Mass Flow | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
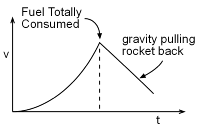
Use Newton's Second Law to sum all the forces acting on the rocket and equate it to the acceleration times mass, ΣF = ma Ff - mg = m (dv/dt) The thrust, Ff, is due to the mass flow of the burning propellant. Using the mass flow equation gives, Ff = -(dmf /dt) vf = (dmf /dt) vfj = cvfj Notice, all motion and forces are only in the y direction. Combining equations for the y-direction, cvf - mg = m (dv/dt) Rearrange to get dv = (cvf /m - g)dt At any time t, the total mass of the rocket and the remaining fuel can be expressed as m = mo - (dmf /dt) t = mo - ct By substituting, the change in velocity, dv, is |
|
|
|
Integration will give an expression for the velocity as The total time required to burn all the fuel is mf = (dmf /dt)ttot = c ttot ttot = mf /c Now that the time needed to burn all the fuel is known, it can be substituted back into the velocity equation to give, where vf = fuel velocity (constant) |
|