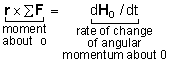| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Angular Momentum | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
|
Angular momentum is analogous to the principle of impulse and momentum. The angular momentum about a point (generally the origin, O) is The distance vector, r, is from the point of rotation to the object. This cross product will produce a vector, H, that is perpendicular to both r and v, as shown in the diagrams at the left. Most problems deal with the angular momentum for an object moving in the x-y plane (about the origin O). Then the angular momentum equation simplifies to Ho = m|r||v| sinθ ez where r is the position vector of the object and ez is the unit vector in the z direction. The relationship between the angular momentum of an object and the external moment applied to the object can be determined by examining the cross product of the position vector and Newton's Second Law, or r × ΣF = r × ma = r × m dv/dt The right-hand side of the this equation equals the time derivative of the angular momentum, d(r × mv)/dt = (dr/dt × mv) + (r × m dv/dt) = (v × mv) + (r × m dv/dt) = r × m dv/dt Thus, the moment of external forces about O equals the object's rate of change of angular momentum about O: Integrating this equation with respect to time gives
If the moment acting on an object about a fixed point O is known, it can be integrated to determine the object's change in angular momentum. If the moment is zero, Ho is constant, i.e. angular momentum is conserved. |
|||||||
| Central-Force Motion |
||||||||
|
If the total force acting on the object remains directed towards a fixed point, such as the origin O, then the fixed point is called the center of motion, and the object is said to be in central-force motion. The position vector r is always parallel to the force, thus the moment is zero: r × ΣF = 0 Hence, for central-force motion, angular momentum is conserved, i.e. Ho is constant. |
||||||||
| Plane Central-Force Motion |
||||||||
|
|
If an object undergoes central-force motion in a plane, then it is said to be in plane central-force motion. If r and v are expressed in cylindrical coordinates then r = rer v = vrer + vθeθ Substituting these into the equation for angular momentum gives Ho = r × mv = rer × m (vrer + vθeθ) = mr vθez This equation indicates that for plane central-force motion, the product of the radial distance from the center of motion and the transverse component of velocity is constant, i.e. r vθ is constant. |
|||||||