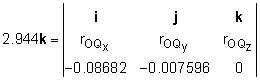Direction of Forces

Although scalars can be used to solve this problem, vector notation will be used. The standard directions will be used for the coordinate system. The two rocket forces that turn the firework are

     F₁ = 0i - Tj + 0k

     F₂ = -Tsinαi + Tcosαj + 0k

where T is the trust, 0.5 lb and α is the misaligned rocket angle of 10^o. The position vectors from point O to each force's point of application are

     r₁ = -3i + 0j + 0k

     r₂ = 3i + 0j + 0k

Equivalent Force and Moment

Calculating Equivalent Force

The system of two forces can be replaced by an equivalent system consisting of a force F_R and couple M_R applied at point O. The force F_R is found by summing the individual forces.

     F_R = ΣF = F₁ + F₂
          = -Tsinαi + T(cosα - 1)j + 0k

Substituting the known values, α = 10^o and T = 0.5 lb, gives

     F_R = -0.08682i - 0.007596j + 0k lb

The moment M_R is the sum of the individual moments.

     M_Ro = ΣM_o = r₁× F₁ + r₂× F₂

The cross products can be written as determinants, giving,

     
        = 0i - 0j + 3T(1 + cosα)k

Substituting the known values gives

     M_Ro = 0i - 0j + 2.977k in-lb

Since all the forces act in the same plane, there is a single force resultant for this problem. The resultant force is the same F_R as before but it is located at a different point Q, which must satisfy the equation

     M_Ro = r_OQ × F_R

Writing this equation in determinant form and substituting known vectors gives,

     2.977k = [0 - r_OQz (-0.007596)]i
                - [0 - r_OQz (-0.08682)]j +
                  + [(r_OQx (-0.007596) - r_OQy(-0.08682)]k

From the i and j terms, r_OQz must be zero. However, the k term gives

     2.977 = -0.007596 r_OQx + 0.08682 r_OQy

From inspecting the diagram, it is noted that point Q was chosen to be directly vertical from O. Thus, the r_OQx must be zero. This gives,

     2.977 = 0.08682 r_OQy

Therefore

     r_OQ = 0i + 34.29j + 0k  in

Applying the single force F_R at the point Q has the same effect as the two original forces F₁ and F₂.