Problem Diagram

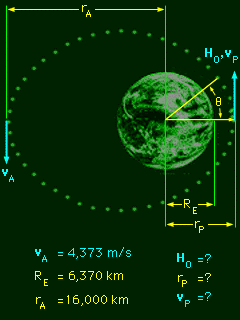
After docking with the Soyuz, the Apollo must re-enter the earth's atmosphere from perigee (the closest point of the orbital path to the earth). If the Apollo is traveling too fast, it will burn up during re-entry.

What is known:

• The mass of the Apollo is m_A = 18.0 Mg.
• At apogee (the furthest point of the orbital path from the earth), the speed of the Apollo is v_A = 4,373 m/s.
• At apogee, the Apollo's distance from the center of the earth is r_A = 16,000 km.
• The radius of the earth is R_E = 6,370 km.

At perigee, what is the Apollo's angular momentum, distance from the center of the earth, and speed?

• Use the equations of angular momentum to determine the angular momentum at apogee, then at perigee.
• Use equations involving the distance from the center of the earth and the transverse velocity (derived from angular momentum) to find the velocity at perigee.