| Ch 4. Moments/Equivalent Systems | Multimedia Engineering Statics | ||||||
|
Moment 2-D Scalar |
Moment 3-D Scalar |
Moment 3-D Vector |
Couples and Equiv. System | Distributed Loads, Intro | |||
| Moment of Force: 3-D Vector | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Position Vectors
|
||
 Position Vectors |
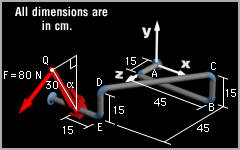
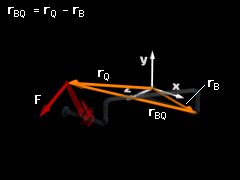
Coordinate systems can be attached to any point, but generally there is one or two points that are more convenient than others. For this problem, the coordiante system is placed at far right edge of the pipes. The position vector from the right edge of the pipe to joint B is rB = rBxi
+ rByj + rBzk The position vector of point Q (location of applied force F) can be determined when the wrench is rotated at an angle of α as rQ = rQxi
+ rQyj + rQzk From vector addition, the position vector from joint B to point Q is rB + rBQ = rQ or |
|
|
|
Force Vector
|
|
|
The system of two forces can be replaced by an equivalent system consisting of a force FR and couple MR applied at point O. The force FR is found by summing the individual forces, F = Fxi + Fyj
+ Fzk |
||
| Moment Vector |
||
 Moment Variation with Angle α |
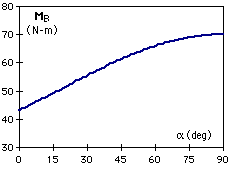
The moment of the force about joint B is given by MB = rBQ ×> F The cross product in determinant form is Expanding the equation gives MB = (rBQy Fz
- rBQz Fy)i + (rBQz Fx
- rBQx Fz)j Substituting the appropriate values and simplifing to determine the moment at joint B gives MB = (2,400 + 3,600 sinα)i
If the magnitude of MB is plotted as a function of the angle α, then the moment is a maximum at α = 90°, with a value of 6,997 N-cm or about 70 N-m. This is approximately 62% greater than the moment at α = 0°. |
|