| Ch 4. Beam Stresses | Multimedia Engineering Mechanics | ||||||
|
Bending Strain and Stress |
Beam Design |
Shear Stress |
Built-up Beams |
||||
| Beam Design | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
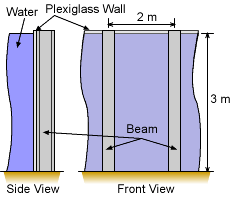
A new aquarium plans a large fish tank with a water depth of 3 meters. One of the walls will be constructed from Plexiglas and supported by vertical I-beams. The beams will be spaced every 2 meters. The water pressure will cause a distributed load on the beams. The beams can be modeled as a cantilever beams since the base is fixed and the top end is free. The minimum weight S type I-beam needs to be specified using the beams listed in the appendix. |
|
| Loading |
||
|
|
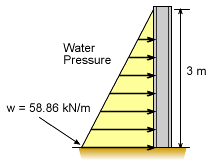
The water will cause a pressure on the wall which is a linear function of the depth. The pressure on the wall will be p = h g ρ where ρ is the water density and g is the gravitational constant, 9.81 m/s2. The maximum pressure will be at the bottom, h = 3 m, p = (3 m) (9.81 m/s2) (1 g/cm3) = (3 m) (9.81 kN/m3) = 29.43 kN/m2 The pressure now needs to be converted to a distributed load on a typical vertical beam. There is one beam for every 2 meters, so the maximum distributed load at the bottom is wmax = (29.43 kN/m2 )(2 m) = 58.86 kN/m |
|
| Moment |
||
|
|
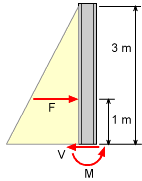
The maximum moment for a cantilever beam is at the base. The distributed load has an equivalent load of F = 0.5 (58.86 kN/m)(3 m ) = 88.29 kN Summing moments at the base gives, ΣMbase = 0 Mmax - (88.29 kN)(1 m) = 0 Mmax = 88.29 kN-m |
|
| Section Modulus |
||
|
Now that the moment is known and the yield stress is given, the section modulus can be determined. There is a factor of safety of 3.0 that will reduce the allowable stress. Srequired = M/σ = 88.29 kN-m / (250,000/3 kN/m2 ) = 1,059 × 103 mm3 Looking at the appendix listing of all S type I-beams (note, SI units) give the lightest beam with at least 1,059 × 103 mm3 as S380 x 74 This beam type has a section modulus of 1,060 × 103 mm3 so it will just barely work. |
||