| Ch 3. Derivatives II | Multimedia Engineering Math | ||||||
|
Higher Order Derivatives |
Related Rates |
Differential |
Newton's Method |
||||
| Newton's Method | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
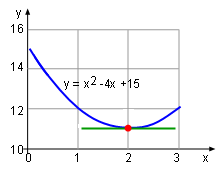
In engineering, many problems require one to find the stationary point or root of a function f(x) = 0. High order functions, such as x10 + 7x9 + 4x7 + 8x4 + 9x3 + 70 = 0, are extremely difficult to solve by hand. However, numerical methods like Newton's method can find the approximate root for such equations. |
||
| Newton's Method |
||
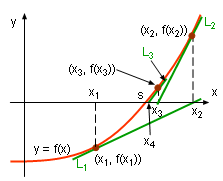 Newton's Method
|
The prerequisite of using Newton's method, also known as Newton-Raphson method, is that the function must be differentiable and point x1, the initial estimate, must be close to a solution of the equation f(x) = 0. Numerical methods require numerous steps use the derivative of the function to "zero in " to the answer. This is done by first constructing function's tangent line L1 from point (x1, f(x1)). Next, find the intersection of the x axis and L1 which is (x2, 0). It is helpful to remember that the equation of a line is y - y1 = m(x-x1) where m is the slope. As the slope of L1 is the derivative of the function and (x1, f(x1)) is a given point, the equation of L1 can be expressed as y2 - f(x1) = f '(x1)(x2 - x1) Since L1 intersects x axis, the value of y2 equals 0. The equation can be simplified to - f(x1) = f '(x1)(x2 - x1) When f '(x1) ≠ 0, x2 is obtained x2 = x1 - f(x1)/f '(x1) |
|
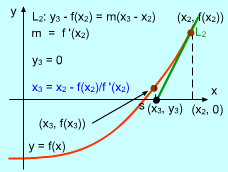 Newton's Method - Second Iteration Newton's Method - Second Iteration |
Next, repeat this iteration from x2. The intersection, x3, of tangent line L2 and x axis, is found. x3 = x2 - f(x2)/f '(x2) By repeating this iteration, a series of points x1, x2, x3, ....xn is obtained. The value of xn+1 is xn+1 = xn - f(xn)/f '(xn) This value approaches to the stationary point of the function. |
|
|
||
| Example |
||
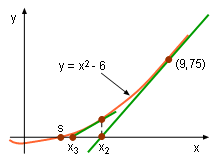 Linear approximation for function y = x2 - 6 |
The concept of Newton's Method can be understand by finding the stationary point around (9, 75) for function y = x2 - 6. To compare with Newton's method later, the exact answer is easily determined. When y = 0, x2 - 6 = 0 Therefore, x = 2.449 and x = -2.449, the stationary point around (9, 75) is x = 2.449. In the diagram it is s = 2.449. Now use the Newton's method to find the stationary point.The slope of the tangent line for function y = x2 - 6 is m = dy/dx = 2x At x = 9 point, m = 2(9) = 18. Recall that the equation for the tangent line is y - y1 = m(x - x1) |
|
| First iteration Substitute (9, 75) and m = 18 into the line equation gives, y - 75 = 18(x-9) When stationary point is the point when y = 0, thus, 0-75 = 18(x-9) so x = 4.833 That is x2 = 4.833. The relative error = (x2 - s)/s = (4.833 - 2.449)/2.449 = 97.3%. This error is too large to accept. Therefore more iterations are needed. |
||
| Second iteration Find the function's value when x2 = 4.833. f(4.833) = (4.833)2 - 6 = 17.358 Substituting (4.833, 17.358) and m = 2x = 2(4.833) = 9.666 into y - y2 = m(x - x2) gives: y - 17.358 = 9.666(x - 4.833) Setting y = 0 gives 0 -17.358 = 9.666(x - 4.833) So x = 3.037. That is x3 = 3.037. The relative error = (x3 - s)/s = (3.037 - 2.449)/2.449 = 24% It is obvious that the relative error reduces and the value approaches real stationary point. If more iterations are done, the accuracy increases. |
||
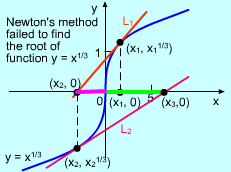
| Example when Newton's Method Fails |
||
|
In the above example, Newton's method was able to find the root of equation x2 - 6 = 0, but in some cases Newton's method can fail for various reasons.Some examples are listed below.
|
|