| Ch 3. Particle Energy Methods | Multimedia Engineering Dynamics | ||||||
|
Work & Energy |
Conservative Forces | Power & Efficiency | |||||
| Power and Efficiency: Velocities | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
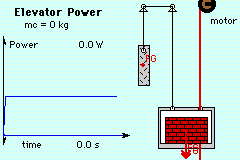
 Elevator Diagram |
To calculate the power required, both the force pulling the elevator up and the elevator's velocity must be determined. The elevator's velocity, ve, is a constant 1 m/s and thus there is no acceleration (dv/dt = a = 0). The mass and dimensions of the elevator are given. |
|
| Counterweight cable tension |
||
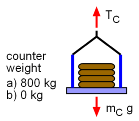 Counterweight FBD |
The counterweight, c, free-body diagram gives Tc = mc g Remember, acceleration is assumed to be zero.
|
|
| Elevator cable tension |
||
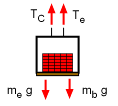 Elevator FBD |
Using the free-body diagram for the elevator, e, and summing the forces in the vertical direction gives Tc + Te = mbg + meg where mb is the mass of the bricks. Combining with the counterweight cable tension gives Te = (mb + mec)g |
|
| Solution of a) |
||
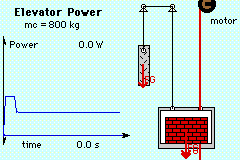 Counterweight = 800 kg |
If the counterweight mass mc is 800 kg, then the tension in the cable is Te = (1000 + 1000 - 800) 9.81 The required power output is Po = Te ve
Motors and mechanical equipment will lose energy from other sources, such as friction. Thus the motor has to deliver more power than what is actually being lifted.The, mechanical efficiency, η, is |
|
| Solution of b) |
||
|
|
If the counterweight mass, mc, is 0 kg, then tension in the cable will be Te = (1000 + 1000 - 0) 9.81 The required power output is Po = Te ve
Considering the motor efficiency, η, gives |
|
Comparison between the elevator with and without the counterweight can now be done. Pc = 800 = 14.73 kW The increase in power without the counterweight is (24.53 - 14.73)/14.73 = 67% |
||