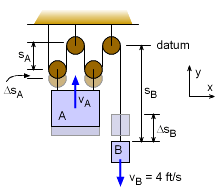
Two blocks are attached to a system with four pulleys. If both blocks are simultaneously released from rest, what is the displacement of block B travel when its velocity reaches 4 ft/s. Assume the pulleys are massless.

Displacement of Objects

Since both displacement and velocity are parameters of the problem, energy can be used to solve the problem.

First, arbitrarily assume a downward displacement for block B, Δs_B, and relate it to the displacement of Block A, Δs_A. This can then be used to relate their velocities. The length of the cable from block B does not change.
     4s_A + s_B = L
     4 Δs_A = Δs_B

Time derivative gives,
     4v_A + v_B = 0 
     v_A = -(4)/4 = - 1 ft/s

The system conserves energy, thus the energy before lease and after release must stay constant.
     T₁ + V₁ = T₂ + V₂
     0 - m_Ags_A - m_Bgs_B
              = -m_Ag(s_A + Δs_A) - m_Bg(s_B - Δs_B)
                               + 0.5m_A v_A² + 0.5m_B v_B²

Cancel terms,
     m_AgΔs_A - m_BgΔs_B = 0.5m_A v_A² + 0.5m_B v_B²

Substitute Δs_A = Δs_B,  v_B = 4 m/s, and v_A = -1 m/s
     50 (Δs_B /4) - 8 Δs_B = 0.5(50/g)(-1)² + 0.5(8/g) 4²
     4.5 Δs_B = (25 + 64) / 32.2

Δs_B = 0.6142 ft