| Ch 3. Particle Energy Methods | Multimedia Engineering Dynamics | ||||||
|
Work & Energy |
Conservative Forces | Power & Efficiency | |||||
| Conserv. Forces/ Potential Energy | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
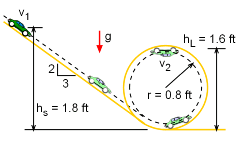
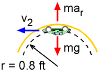
The initial velocity needs to be determined so that the unattached car will stay on the track around the 360° loop. There must be enough centrifugal force to counteract gravity at the top of the loop. This force is due to the tangential velocity of the car. As shown in the free-body diagram, the gravitational acceleration must be counteracted by the centrifugal acceleration, or mar = mg Radial acceleration is related to the tangential velocity as ar = v2/ρ Substituting gives, v22 = rg Now that the car's velocity at the top of the loop is known in terms of the radius, the Conservation of Energy can be applied. |
|
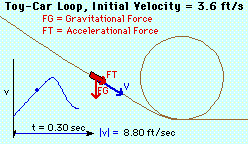 Initial Velocity = 3.6 ft/s |
V1 + T1 = V2 + T2 Using the previous v22 = rg results gives v12 + 2(1.8 ft) g = rg + 2(1.6 ft) g v1 = 3.59 ft/s |
|