| Ch 3. Particle Energy Methods | Multimedia Engineering Dynamics | ||||||
|
Work & Energy |
Conservative Forces | Power & Efficiency | |||||
| Principle of Work and Energy | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
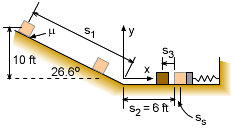
There are three possible places where a package can stop. All three possibilities need to be examined:
Each possible solution can be solved using energy. Assuming that the package freely slides, then the gravitational potential energy less any energy loss due to friction will equal the change in kinetic energy. |
|
| Check if Package Slides |
||
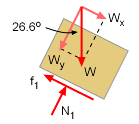 Check if Package will Slide |
The first step in all sliding problems is to check if the object will actually slide. For motion to occur, the weight component of the object parallel to the surface, Wy, must be larger than the maximum friction force, f1. f1 = μ N1 = 0.3 W cos26.6 The weight component parallel to surface is, Wx = W sin26.6 = 50 (0.4478) = 22.39 lb Thus, Wx > f1, and motion will occur. The acceleration of the object, Wx - f1 = m ax, could be determined, but since energy methods will be used, it will not be needed. |
|
| Case a) Stops Before Striking Bumper |
||
Lets first check the simplest possibility, that the package will stop before reaching the spring bumper due to friction. Apply the Principle of Work and Energy: T1 + ΣU1-2 = T2 In this case, both the initial velocity v1 and the final velocity v2 are zero, and thus both T1 and T2 are zero. ΣU1-2 = 0 |
||
|
|
There are two possible sources of energy change between points 1 and 2, gravity, Ug, and friction, Uf. Work due to gravity Ug is the weight times the vertical distance, Ug = mgh = mg (10) The friction energy loss, Uf, must consider both the slope distance, s1, and the horizontal distance s2. Note, that friction energy is negative since the energy is lost to heat. Uf = - μ N1 s1 - μ N2 s2 where s1 = 10/sin26.6 = 22.3 Substituting and canceling mg gives, 10 - 0.3 cos26.6 (22.3) - 0.3 s2 = 0.0 The horizontal distance required for package to stop, s2, is s2 = 13.4 ft Since 13.4 ft > 6 ft, the package will not stop before it hits the bumper. |
|
| Case b) Stops While Compressing Spring |
||
|
This is not likely since previous results showed that the package will need 13.4 ft to stop. The package will rebound from the spring and then stop. |
||
| Case c) Rebounds After Striking Bumper |
||
| Next, assume the package will hit the bumper, compress the spring, reverse direction and move back towards the slope. However, to simplify the calculations, it is assumed the package does not go back up the slope. If the solution is greater than 6 ft (after considering package width), then the package will go up the slope, and the solution will need to be redone (lets hope not). | ||
|
|
There are a number of distances than need to be defined. The slope distance, s1, is still the same, but lets define s2 as the horizontal distance from the slope to the uncompressed spring. Next, lets set s3 to be the rebound distance from the spring and ss be the compressed spring distance. All these distances are shown on the diagram at the left. The distance ss must be calculated before the rebound distance s3 can be determined. Part 1): Use the Principal of Work and Energy over distances s1, s2, and ss: T1 + ΣU1-2 =
T2 where v1 = 0 v2
= 0 Substituting the known values gives 5 (10) - 0.5 (50) ss2 - 0.3 (44.71) (22.33) Solving gives the solution for how far the spring is depressed before the package comes to rest, ss = 1.824 ft (other root is negative, -2.424 ft) Part B): Now that spring compressed distance is known, the total distance the package rebounds can be determined. The energy equation can be used again, but analysis is from the compressed position (v = 0) and the final position (v = 0). There are two distances involved, ss and s3. Σ(Us + Uf) = 0 (since comes to rest) s3 = 3.70 ft (or x = 6 - 3.7 = 2.4 ft) Notice, the weight (W = mg) does not cancel and thus the weight does effect the final solution, even though it will be small if the spring compression distance is small. |
|