| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| Dot Products | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Vector Multiplication |
||
|
In the previous two sections, addition and subtraction of 2-D and 3-D vectors were illustrated. When "multiplying" two vectors, a special types of multiplication must be used, called the "Dot Product" and the "Cross Product". This section deals with only the dot product. The cross product is presented in a later section. |
||
| Dot Product |
||
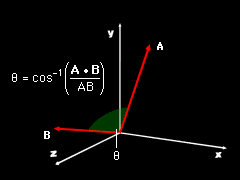 Dot Product Angle |
The dot product of two vectors A and B is defined as the product of the magnitudes A and B and the cosine of the angle θ between them: A • B = |A| |B| cosθ The dot product can also be calculated by A • B = Ax Bx + Ay By + Az Bz where vectors A and B are given as A = Ax i + Ay j + Az k |
|
| Applications of the Dot Product |
||
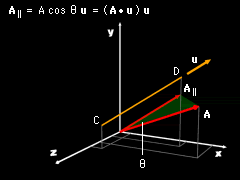 Component Parallel to a Line
|
Using the dot product, the angle between two known vectors A and B, can be determined as If the direction of a line is defined by the unit vector u, then the scalar component of the vector A parallel to that line is given by A|| = A • u The vector component parallel to that line is given by A|| = (A • u) u Using the properties of vector addition, or the Pythagorean theorem, we can also determine the scalar and vector components of A perpendicular to the line: |
|
