| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| Dot Products | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Unit Vector Parallel to AB |
||
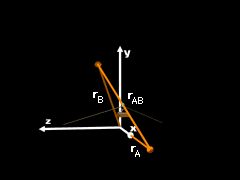 Adding rA and rB |
The direction of line AB is defined by the position vector rAB, which can be found from vector addition, rA + rAB
= rB = (39 - 175)i + (70 - 0)j + (29 - 0)k = -136i + 70j + 29k The unit vector in the direction of rAB can be determined by dividing rAB by its magnitude rAB, rAB = (-1,362 + 702 + 292)0.5 = 155.7 m uAB = rAB/rAB = -0.8736i + 0.4496j + 0.1863k |
|
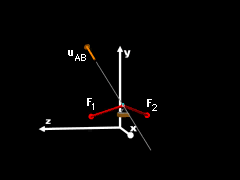 Total Force on Trolley |
||
| Total Force on Trolley |
||
|
Add the two forces applied to the trolley to find the total force, FT = F1 + F2 = -1,863i - 437.7j - 83.2k N |
||
| Component Parallel to uAB |
||
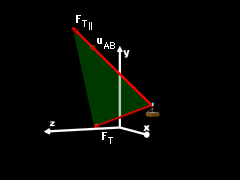 Force Component to Parallel to uAB |
The scalar component of the total force parallel to the direction uAB can be found by using the dot product, FT|| = FT • uAB = -1,863 (-0.8736) - 437.7 (0.4496) - 83.2 (0.1863) = 1,415 N This is just the magnitude of the total force acting in the direction of the cable AB. This can also be represented as a vector by multiplying this scalar component by the unit vector uAB, giving, FT|| = FT|| uAB = -1,236i + 636.3j + 263.7k N The magnitude or FT|| has not changed but is now represented as a vector. |
|