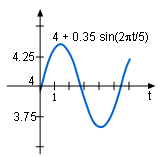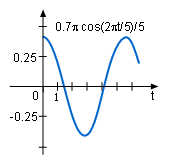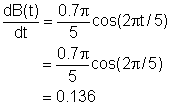| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Chain Rule | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
|
The brightness of Delta Cephei increases
and decreases according to its brightness function Substitute the average brightness of the star 5 days into the brightness function, B(t) = 4 + 0.35 sin(2πt/5) Let f(t) = 2πt/5, then B(t) = 4 + 0.35 sin(f(t)) Using the to Chain Rule, the rate of changes for the brightness of Delta Cephei is After a day the brightness is |
|