| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Hydrostatic Force -Curved Surface | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
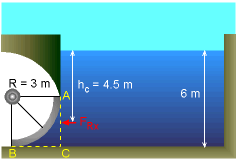
In order to determine the magnitude of the resultant force exerted on the curved surface AB, first find its force components FRx and FRy. The horizontal projection of the curved surface AB is the plane area AC. The x-component of the resultant force is given by the normal force acting on this plane area. That is, FRx = ρghc AAC Note that hc is the vertical distance to the centroid of plane area AC. |
|
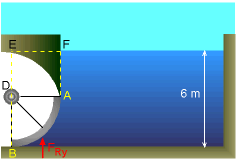 Y-Component of the Resultant Force |
The y-component of the resultant force is the weight of the water directly above the curved surface (i.e., imaginary volume ABEF). FRy = ρg
VolABEF = ρg (VolADEF +
VolABD) Hence, the resultant force is given by FR = (FRx2 + FRy2)0.5 |
|
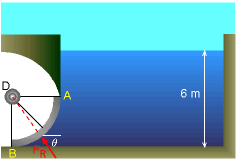 Resultant Force and its Line of Action |
And the angle θ is given by θ = tan -1 (FRy / FRx) Also, the resultant force FR has to pass through point D since all the pressure forces are perpendicular to the curved surface. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.