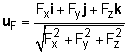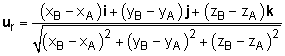| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| 3-D Vectors | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
Cartesian Components |
|
|
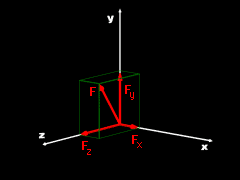
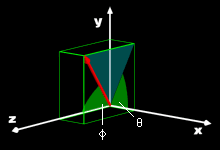
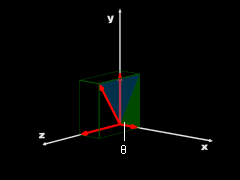
Recall, from the previous section, a vector in the x-y plane in can be written in Cartesian notation as, F = Fxi + Fyj Here i and j are unit vectors in the x and y directions. Likewise, a vector can be written in the three dimensional x-y-z space in Cartesian form, F = Fxi + Fyj + Fzk The new component, k is the unit vector in the z direction. The components Fx, Fy, and Fz can be determined from the magnitude and direction of F, Fx = F cosθx
The angle θi is the angle that F makes with the i axis as shown in the diagram at the top left.
|
||
 Right Hand Coordinate System |
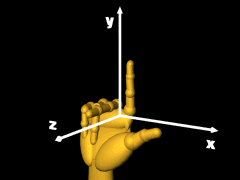
Right-handed Coordinate System |
|
The order of the x-y-z coordinates does matter. If the three coordinates are aligned so that the thumb is in the x-direction when the first finger is in the y-direction and the second finger is in the z-direction, then it is called a right-handed coordinate system. Otherwise, it would be a left-handed coordinate system. Engineering always uses right-handed coordinate system. There is nothing wrong with a left-handed system, but all books, equations and technical papers use a right-handed system for convention. |
||
| Vector Addition |
||
|
|
Addition of 3-D vectors is the same as for 2-D except that three components must be added instead of two. If two vectors F1 and F2 exist, then the addition of F1 and F2 is, FR = F1+ F2 FR = (F1x + F2x)i + (F1y + F2y)j + (F1z + F2z)k The magnitude of the resultant vector is determined by applying the Pythagorean theorem, FR = ( FRx2 + FRy2 + FRz2 )0.5 The direction cosines are useful in some problems to identify each direction component. They are given as, cosθx = FRx /FR |
|
| 3D Unit Vector |
||
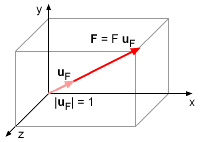 3-D Unit Vector |
General unit vectors can be determined in 3D using the definition of unit vectors, as uF = F/F Substituting vector notation and magnitude for F, gives This relationship is useful when the direction of the vector is needed. |
|
| Position Vectors |
||
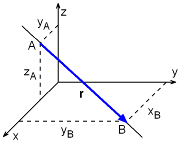 Position Vector |
In statics, force and moment vectors are the most commonly but many times a position vector is needed to help determine the direction of the force or moment vector. Position vectors are the same as all vectors, but they describe direction and distance, r = xi + yj + zk where x, y, and z are distances (scalars). Generally, position vectors are determined by its two end points, giving r = (xB - xA)i + (yB - yA)j + (zB - zA)k The directional unit vector for a position vector is ur = r/|r |
|
|
|
Spherical Coordinate Angles |
|
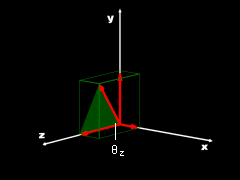
If the direction of the vector is defined by the two angles θ and φ, (shown at the left) as is commonly done in spherical coordinate systems, then the components are given by Fx = F sinφ cosθ The spherical angles θ and φ are given by, φ = cos-1 FRz /FR θ = sin-1 FRy /(FR sinφ) |
||