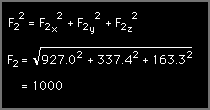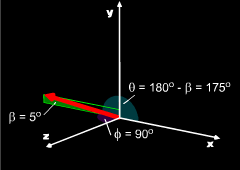
With the x-y-z axes oriented as shown, the direction of the normal propeller is defined by the spherical angles θ and φ:

     θ₁ = 175^o
     φ₁ = 90^o

The magnitude is F₁ = 1000 lbs. The cartesian components can be calculated by,

    F_1x = F sinφ₁ cosθ₁
         = 1000 sin90 cos175 = -996.2 lb
    F_1y = F sinφ₁ sinθ₁
         = 1000 sin90 sin175 = 87.2 lb
    F_1z = F cosφ₁
         = 1000 cos90 = 0 lb

Vector F₁ can be written in Cartesian notation as

     F₁ =-996.2i + 87.2j + 0k lb

Summing Components 

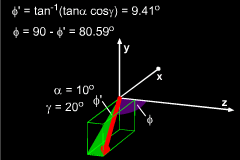
For the bent propeller, the spherical angles are more difficult to find but can be found from geometry. The animation at the left shows how to find these angles. They are,

     θ₂ = 200^o
     φ₂ = 80.59^o

The magnitude F₂ is given as 1000 lb. The component magnitudes are

    F_2x = F sinφ₂ cosθ₂ = -927.0 lb
    F_2y = F sinφ₂ sinθ₂ = -337.4 lb
    F_2z = F cosφ₂ = 163.5 lb

Vector F₂ can be written in Cartesian notation as

     F₂ =-927.0i - 337.4j + 163.5k lb

Next, add F₁ and F₂ to get the total force on the boat.

     F_T = F₁ + F₂

         = -1923.2i - 250.2j + 163.5k