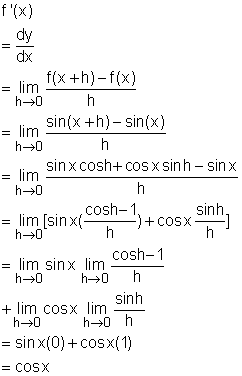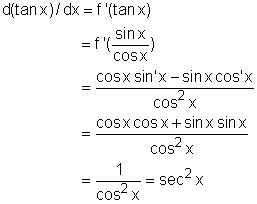| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Trigonometric Functions | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||||
| The main topic of this section is derivative formulas for trigonometric functions. | ||||||||||||||||
| Trigonometric limits at Specific Angle |
||||||||||||||||
| In order to compute the derivatives of trigonometric function, some of the trigonometric limits need to be mentioned first. |
||||||||||||||||
| Derivatives of Trigonometric Functions |
||||||||||||||||
 sin'x = cos x |
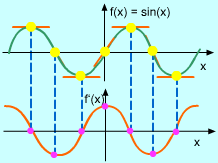
The derivatives of trigonometric functions can be proven by use of the definition of derivative and the trigonometric limits. Proof If f(x) = sinx, then Now that d(sinx)/dx equals cosx has been proven, what does d(sinx)/dx look like in graph? Is it the same as cosx? The value of the derivative at any value of x can be estimated by drawing the tangent at the point (x, f(x)) and estimate its slope. For example, at the point of x equals 0, draw the tangent at this point and estimate its slope to be around 1, so d(sinx)/dx = 1. Now plot the point (0, 1) on the graph of df/dx or f '. By repeating this procedure at different points, the graph of f ' can be drawn and will resemble a cosine curve. The correction of the graph is confirmed by formula (1). |
|||||||||||||||
Using the definition of derivative and the trigonometric limits, the formula d(cosx)/dx = -sinx (2) can be proved. |
||||||||||||||||
According to the formula (1) and (2), the derivative of tangent function can be found. d(tanx)dx = sec2 x Proof If f(x) = tanx |
||||||||||||||||
The derivatives of the csc, sec, and cot are listed below: d(secx)/dx = secx tanx d(cscx)/dx = -cscx cotx d(cotx)/dx = -csc2x |
||||||||||||||||
The follow table is a list of most commonly used derivatives of the trigonometric functions.
|
||||||||||||||||