| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| Scalars, Vectors and Operations | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Scalars vs. Vectors |
||
|
|
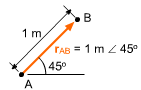
Any quantity that is represented by a positive or negative number is called a scalar. Mass, volume, and distance are examples of scalars. Scalars are generally represented by letters in plain type such as A = 5 kg. Mathematical operations on scalars follow the laws of elementary mathematics and algebra. A vector represents a quantity that has both magnitude and direction. Examples of vectors include position, force, moment (torque) and velocity. Mathematical operations involving vectors follow the rules of vector algebra, which is discussed below. Vectors are generally represented graphically by an arrow. The length of the arrow represents the magnitude, and the direction is defined by the angle between the vector and some reference axis. Vectors are represented symbolically by a boldface letter such as B = 10 km north. The magnitude of a vector is a positive quantity and is written as a scalar such as B = |B|. In the next section, 2-D Vectors, vector notation will be presented which makes working with vectors easier. |
|
| Multiplication of a Vector and a Scalar |
||
|
Vectors Multiplied by Scalars |
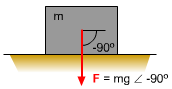
If the vector B is multiplied by the scalar a, the result is the vector aB. If the scalar a is negative, then the vector is in the opposite direction. Division of the vector B by a scalar a can be described as a special case of multiplication. |
|
| Graphical Vector Addition |
||
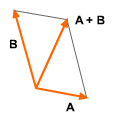 Parallelogram Law 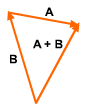 Vector Addition |
Two vectors, A and B, can be added graphically by using the parallelogram law. The vectors are joined at the tails and parallel lines are drawn from the head of each vector. The intersection point of the parallel lines is the head of the vector A + B. The vectors A and B can also be added by joining them in a head-to-tail fashion. When adding B to A, the tail of B is placed at the head of A. The result R extends from the tail of A to the head of B. We can also find the same result by adding A to B. This means that vector addition is commutative, A + B = B + A |
|
| Graphical Vector Subtraction |
||
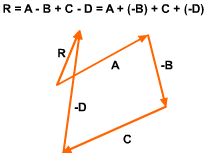
Vector subtraction can be written as a special case of vector addition, A - B = B + (-A) |
||
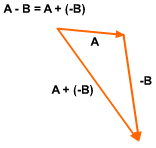 Vector Subtraction |
|
|