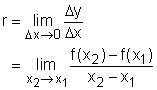| Ch 2. Derivatives I | Multimedia Engineering Math | ||||||
|
Derivative Formulas |
Trigonometric Functions |
Differentiability |
Chain Rule |
Implicit Differentiation |
|||
| Derivative Formulas | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||||||||||||||||||||
| The problems involving rate of changes exist in many area of engineering research. Since this type of limit happens so widely, it is given a special name - derivative. | ||||||||||||||||||||
| Derivatives |
||||||||||||||||||||
|
The notation of derivative is f '(a). The derivative of a function f at a given point a is defined as: The definition does assume that the limit exists. In order to extend this definition, let x = a + h, substitute x into f '(a) and will get |
|||||||||||||||||||
|
||||||||||||||||||||
| Explanation of the Derivative |
||||||||||||||||||||
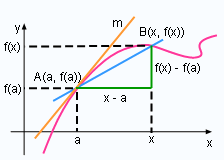 Tangent |
A good way to understand derivatives is to think about a tangent line. According to the definition of the tangent line to a curve y = f(x) at point A(a, f(a)), the tangent line can be written as: Notice that this definition is the same as the definition of derivative f '(a). In other words, the tangent line to y = f(x) at point A(a, f(a)) is the line that passes through (a, f(a)) and whose slop is equal to the derivative of f at a. |
|||||||||||||||||||
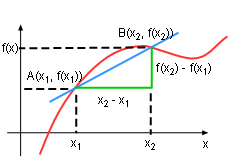 Rate of Change |
In a previous section, the concept of rate of change was introduced. Is it related to derivative? The answer is yes. In a small interval [x1, x2], the changes in x is Δx = x2 - x1 The corresponding change in y is Δy = y2 - y1 The instantaneous rate of change is According to equation (3), r is the derivative of f(x) at x1 |
|||||||||||||||||||
| Derivative
Formulas
|
||||||||||||||||||||
| Calculating derivative according to its definition is tedious. Some rules have been developed for finding derivatives without having to use the definition directly. | ||||||||||||||||||||
|
|
|||||||||||||||||||