| Ch 2. Vectors | Multimedia Engineering Statics | ||||||
| Scalars & Vectors |
2-D Vectors |
3-D Vectors |
Dot Products |
||||
| Scalars, Vectors and Operations | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Algebraic Solution |
||
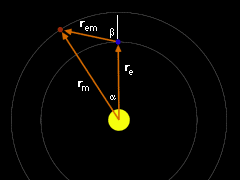 Problem Diagram
|
The position vector from the Sun to Earth is re = re Ð 0o (counter-clockwise from vertical) = 150 × 106 km Ð 0o The position vector from the Sun to Mars: rm = rm Ð α = 207 × 106 km Ð 30o The difference between re and rm is the vector from Earth to Mars. Using the head-to-tail method gives, rm = re + rem This equation can be rearranged to give the unknown position vector rem, rem = rm
- re Subtracting the vectors, gives rem = 107.56 × 106 km
Ð 74.21o |
|
| Geometric Solution |
||
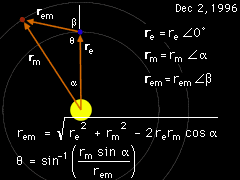 Problem Distance and Angle |
The problem can also be solved using pure geometry. First, define the position vector from Earth to Mars using the equation rm = rem Ð β Next, form a triangle with the three vectors and use the Law of the Cosine, rem = (re2 + rm2 - 2re rm cosα
)0.5 Then the internal angle θ, can be determined using the Law of the Sine, rem / sinα = rem / sinθ θ = sin-1 (rem sinα /rem ) = 105.79o Finally, the desired angle β is β = 180o - θ = 74.21o The position vector from Earth to Mars is rem = 107.56 × 106 km Ð 74.21o |
|
| Comments |
||
| This problem could also be solved using standard vector notation with unit vectors, i and j. Vector notation is introduced in the next several sections and is used extensively throughout Statics. | ||
