| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Continuity | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| In this section, the concept of continuous and discontinuous is introduced. Various theorems related to continuous function will be discussed. | ||
| Continuous |
||
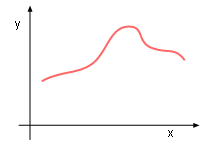 Continuous Function Example |
If then function f(x) is continuous at a.
|
|
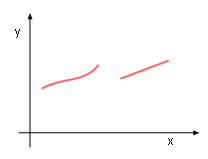 Discontinuous Function Example |
||
| Discontinuous |
||
| If f(x) is not continuous at point a, then f(x) is discontinuous at a. In other words, f(x) has a discontinuity at point a. | ||
| Theorems about Continuous |
||
In this segment, some theorems are introduced to justify whether a function is continuous or not.
|
||
| Intermediate Value Theorem |
||
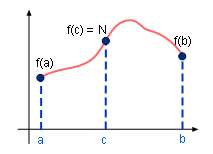 Explanation of Intermediate Value Theorem< |
In order to justify whether a value will fall in a specific range or not, intermediate value theorem is introduced. Assume:
|
|
| Corollary of Intermediate Value Theorem |
||
 f(x) = 0 has 5 roots in [a, b] |
Corollary of Intermediate Value Theorem is a theorem used to verify whether a function has at lease a root or not. Assume:
then the equation f(x) = 0 has at least one root in the open interval (a, b). |
|
|
||
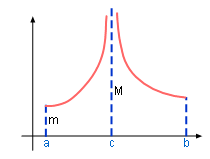
| Extreme Value Theorem |
||
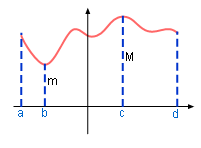 Continuous function with minimum and maximum value |
This is a theorem that can be used for one variable. If f(x) is continuous on [a, b], then f(x) takes on a least value m and a greatest value M on the interval.
|
|
| Theorem |
||
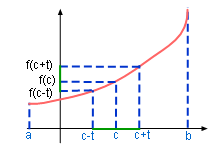 Theorem example |
If f(x) is continuous at point c and f(c) > 0 then there is a positive number t such that, whenever c - t < x < c + t then f(x) > 0. |
|