| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Continuity | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
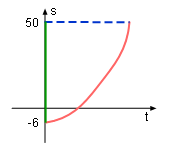 The Elevation Function (Unit: feet) |
Jim moves along an elevation function: He starts from 6 feet below sea level and end at 100 feet
above sea level. When will he pass through sea level? The unit for distance
is feet and the unit for time is minute.
According to corollary of intermediate value theorem, t2 - t - 6 = 0 (t + 2)(t - 3) = 0 Thus, Jim will pass through sea level when t = 3 minutes. |
|
| Discussion |
||
 Function with more than one intersection with sea level |
In order to apply the corollary of intermediate value theorem, the elevation function must be continuous. In the solution of this case, "The Elevation Function" diagram is used to verify the function's continuity. Another method is to apply the continuous theorem. Since this function is a polynomial function, it is continuous. Theorems are important because they lay the foundations for solving problems. In this particular case, there is only one intersection between sea level and the elevation function. As a matter of fact, if the distance function changes, there may be more than one intersections. | |