| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Limit of a Function | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Function |
||
|
If the quantity of y is determined
by another value x, then y is a function of x. If f denotes the
function, then the formula y = f(x) indicate y depends on x. Thus y is
a dependent variable and x is a independent variable. An
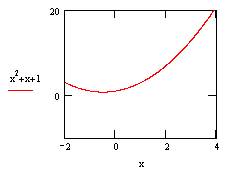
example
of a function would be: |
|
|
||
| Limit of a Function |
||
If for each positive ε, no matter how small, there is a corresponding positive δ such that if then In this situation, the limit of f(x) is A as x approaches a, and it can be written as: |
||
| Limits Involving Infinity |
||
| In this segment, three kind of situations will be discussed. | ||
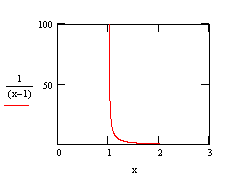 The limit of f(x) is infinity when x approaches 1 |
|
|
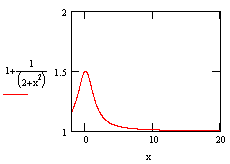 The limit of f(x) is 1 when x approaches +∞ |
|
|
 The limit of f(x) is -∞ when x approaches -∞ |
|
|
 Summary |
Summary |
|
| This section introduces limit of a function and three cases involving infinity. When discussing limit of a function, it must be the limit of a specific point. | ||