| Ch 1. Particle General Motion | Multimedia Engineering Dynamics | ||||||
|
Position, Vel & Accel. |
Accel. vary w/ Time |
Accel. Constant | Rect. Coordinates | Norm/Tang. Coordinates | Polar Coordinates |
Relative Motion |
|
| Line Motion: Acceleration with time | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
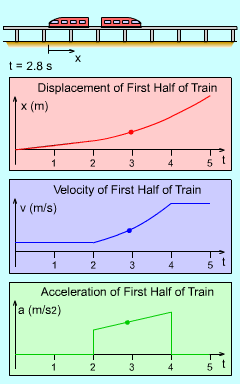 Train Motion |
When integrating the acceleration to determine the velocity and position, the initial conditions must be specified. The lower limits of integration will be vo = 50 m/s to = 2 s When the acceleration is integrated, the expression for the velocity, as a function of time, becomes v(t = 4) = 62 m/s The next step is to integrate the velocity. However, it is important that v(t) is integrated and not the velocity at 2 seconds, 62 m/s. This is a common mistake. Integrating the velocity function, v(t), gives an expression for the position as a function of time, x(t = 4) = 110.7 m Note that the initial position xo was set to zero when to = 2 so that the equation for x(t) gives the change in position starting at t = 2. |
|