| Ch 1. Limits | Multimedia Engineering Math | ||||||
|
Limit of a Sequence |
Limit of a Function |
Limit Laws |
Continuity |
Rate Change |
|||
| Limit of a Sequence | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - CASE STUDY SOLUTION |
||
|
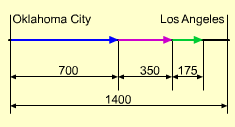
Tom and Mary will drive 1400 miles. On each day they will
drive half of the remaining distance. How long will it take them to get
into 10 miles of their destination.
In each day, Tom and Mary will drive: a2 = 1400(1-1/2)(1/2) = 1400(1/4) a3 = 1400(1-1/2 - 1/4)(1/2) = 1400(1/8) a4 = 1400(1-1/2 - 1/4 -1/8)(1/2) = 1400(1/16) ..... an = 1400(1-1/2 - 1/4 -1/8
-...- 1/(2n))(1/2) |
|
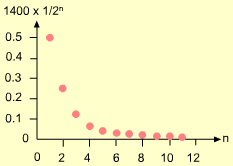 Remaining Distance Sequence |
Therefore the distance remaining is:
d1 = 1400(1/2) d2 = 1400(1-1/2)(1/2) = 1400(1/4) d3 = 1400(1-1/2 - 1/4)(1/2) = 1400(1/8) d4 = 1400(1-1/2 - 1/4 -1/8)(1/2) = 1400(1/16) . dn = 1400(1-1/2 - 1/4 -1/8 -...-
1/(2n))(1/2) |
|
It can be seen that a sequence can be formed: The physical meaning is: for the sequence 1/2n, the remaining
driving distance is 0 when the driving days goes to infinite. |
||