| Ch 7. Centroid/Distributed Loads/Inertia | Multimedia Engineering Statics | ||||||
|
Centroid: Line Area Vol |
Centroid: Composite | Distributed Loads | Area Moment of Inertia | ||||
| Centroid: Line, Area and Volume | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
| Introduction |
||
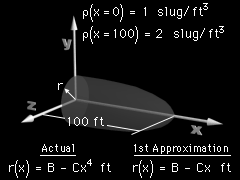 Geometry Diagram |
In order to determine a submarine's buoyancy characteristics, designers must accurately determine the centroid, center of mass, and center of gravity for various parts of the sub. What is known:
|
|
| Question |
||
|
|
As a first approximation, assume the nose code is a simple cone shape (D = 1 in the above equation). Where is the centroid, center of mass, and center of gravity? |
|
| Approach |
||
|
||
Practice Homework and Test problems now available in the 'Eng Statics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
