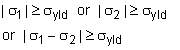| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Failure | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
| Example |
||
|
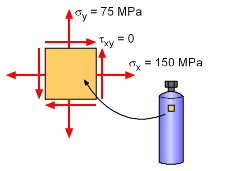
During testing, a thin-walled tank was pressurized with gas and the stresses in the x and y direction were found to be σx = 150 MPa, σy = 75 MPa, and τxy = 0. However, in actual use, the tank must also withstand a torque on the cap that will introduce a possible shear stress in the tank walls. This shear stress is in addition to the stresses due to the tank pressure. What is the maximum torque that can be applied if the vessel material can only withstand a shear stress of 100 MPa? The wall thickness is 15 mm and the outside diameter is 35 cm. Also, the maximum allowable shear stress for the vessel material is 100 MPa. |
|
| Solution |
||
|
|
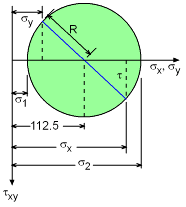
Mohr's circle can be used to understand the solve for this stress state by first finding the largest radius R for which the shearing stress does not exceed 100 MPa and then determine the allowable torque. To draw the Mohr's circle, first the center should be determined. Since, (σx + σy)/2 = (150 + 75)/2 = 112.5, this will be at (112.5 , 0). Assuming a radius R, the Mohr's circle is plotted on the left. From the diagram principal stresses are, σ1 = (σx + σy)/2 - R σ2 = (σx + σy)/2 + R where R = | (σ1 - σ2)/2 | |
|
The goal is to determine the largest radius R for which the shear stress does not exceed 100 MPa. This can be found using "Maximum Shear Stress Theory" that states that for any combination of loading for σ1 and σ2, the shear stress cannot exceed σyld/2 = τmax. This condition gives three separate possible situations that need to be checked, In this problem, the maximum allowable shear stress is given, and not the yield stress. However, the yield stress is simply two times the yield stress for a uniaxial test. The three conditions become, 1st: | σ1 | = σyld = 2τmax = 2(100) 2nd: | σ2 | = σyld = 2τmax = 2(100) 3rd: | σ1 -σ2 | = σyld = 2τmax = 2(100) |
||
|
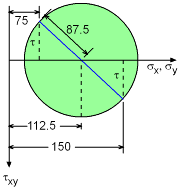
Comparing these three situations, the maximum value of R is the minimum of above three. R = 87.5 MPa From the Mohr's Circle diagram corresponding torsional shear stress is found as, τ = ( R2 - (112.5 - 75) 2 )1/2 = 79.06 MPa Hence, the torque that will cause this torsional shearing stress, T = τJ / r |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.