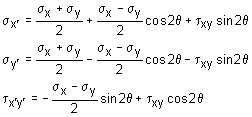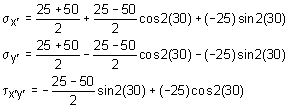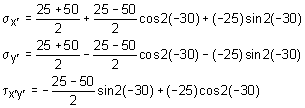| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Plane Stress | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
|
|
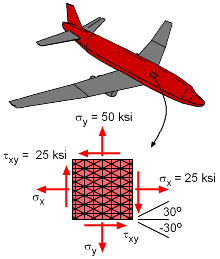
A plane fuselage undergoes both a pressure and twist load. This causes a tension stress in both the longitudinal and circumferential directions and a twisting load or a shear stress. If a stress element is cut from the fuselage, the induced stresses can be shown in a common x-y coordinate system. This longitudinal, or x-direction would be 25 ksi. The circumferential or y-direction would be 50 ksi. The shear stress would be 25 ksi. These stresses are shown in the diagram at the left. The shear arrows in the diagram are in the negative direction, and thus the shear is a negative shear stress. |
|
| Stresses in the +30o Fiber Direction |
||
|
|
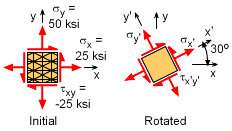
The stresses are requested in both the +30o and -30o. For the +30o, the initial stress element is shown at the left with the positive directions and thus the shear stress is negative. The stress element needs to be rotated 30o in the positive direction. Using the stress transformation equations, the stresses in the new x'-y' coordinate system are Simplifying gives σx´ = 37.5 - 12.5(0.5) - 25(0.8660) = 9.600 ksi σy´ = 37.5 + 12.5(0.5) + 25(0.8660) = 65.40 ksi τx´y´ = 12.5(0.8660) - 25(0.5) = -1.675 ksi |
|
|
|
Stresses in the -30o Fiber Direction |
|
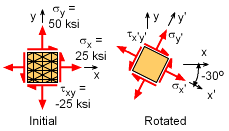 Initial and -30o Rotated Stress Element |
The method to find the stresses in the -30o is the same as for the +30o. Starting with the basic stress transformation equations, gives Simplifying gives σx´ = 37.5 - 12.5(0.5) - 25(-0.8660) = 52.90 ksi σy´ = 37.5 + 12.5(0.5) + 25(-0.8660) = 22.10 ksi τx´y´ = 12.5(-0.8660) - 25(0.5) = -23.33 ksi |
|
|
|
||
| Any Angle |
||
|
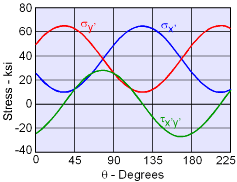
It is interesting to plot the changing stresses as a function of angle. As expected, the stresses vary in a periodic cycle. Due to the double angle trigonometry terms in all three equations, the period is 180o. |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.