| Ch 10. Parametric Equations | Multimedia Engineering Math | ||||||
|
Parametric Equations |
Tangents and Areas |
Arc Length | Surface Area | ||||
| Arc Length | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Hengzhong Wen |
| Chean Chin Ngo |
| Meirong Huang |
| Kurt Gramoll |
| ©Kurt Gramoll |
| |
||
| Introduction |
||
|
|
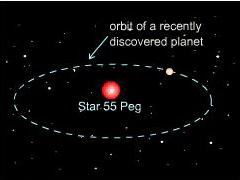
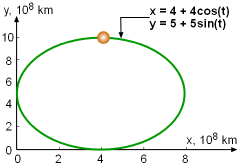
Dr. Smith, a scientist at the Jetway Propulsion
Laboratory, has recently discovered a planet orbit around a distant solar-type
star named 55 Peg. The planet's path is found similar to an ellipse as
shown in the figure. For a report on the new planet, he needs to estimate
the distance traveled by the planet during a complete orbit. |
|
| Questions |
||
| Determine the arc length of one complete orbit. |
||
| Approach |
||
|
||