| Ch 3. Fluid Kinematics | Multimedia Engineering Fluids | ||||||
|
Flow Descriptions |
Steady & Unsteady |
Streamlines, Streaklines |
Velocity & Acceleration |
Irrotational Flow |
|||
| Steady and Unsteady Flows | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Water/Air Tables |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Chean Chin Ngo |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
|
In this section, the discussion is on the difference between steady
and unsteady flow. |
||
| Steady Versus Unsteady Flow |
||
|
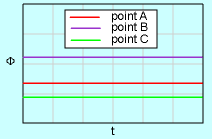
For steady flow, all fluid flow properties (e.g., velocity, temperature, pressure, and density) are independent of time. That is, where Φ represents a fluid property. The properties, however, may vary from point to point, which means that they could be a function of space (i.e., T = T(x, y, z), p = p(x, y, z) and ρ = ρ(x, y, z)). In the study of fluid mechanics it is often assumed that the flow is steady to simplify the analysis but yet give a realistic representation of the real flow field. This is particularly true of basic books on Fluid mechanics, such as this eBook. On the other hand, most flows encountered in real world applications are unsteady flows. It should be noted, steady flow does not mean the velocity and accelerations are constant. Flow in a curved pipe or through a nozzle may be steady, but the velocity and/or acceleration is not constant. This is a common misconception based in part on particle dynamics for rigid bodies. |
|
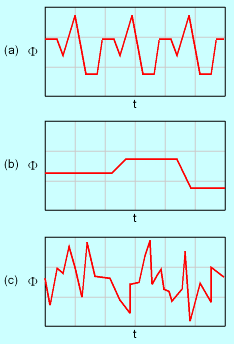 Unsteady Flow: (a) Periodic Flow, (b) Non-Periodic Flow and (c) Random Flow |
For unsteady flow, the fluid properties are function of time (i.e., T =
T(x, y, z, t), p = p(x, y, z, t) and ρ = ρ(x, y, z, t)). Unsteady flows can be further divided into periodic flow, nonperiodic
flow and random flow. The graphical representations of these flows
are given in the figure. For periodic flow, the property change is repeated
in a predictable manner whereas the fluid motion and properties are difficult
to predict in random flow as in turbulent flow. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.