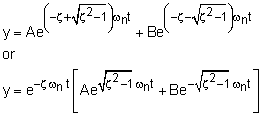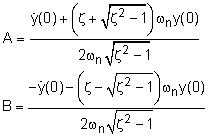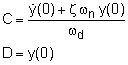| Ch 10. Vibrations | Multimedia Engineering Dynamics | ||||||
| Free Vibs. Undamped | Free Vibs. Damped | Forced Vibration | Energy Method | ||||
| Free Vibrations- Damped | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
|||||
|
|
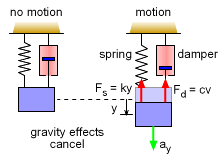
In most mechanical systems, there is some type of damping effect when vibrations occur. It could be air or fluid resistance, shock absorber, or even molecule interactions. This damping effect can be effectively modeled as a force that is proportional to the objects velocity. This type of device is usually called a damper. |
||||
|
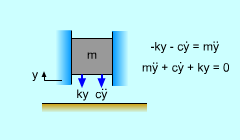
Similar to the simple mass-spring system (undamped) presented in the previous section, the equations of motion of an mass-spring-damper system (damped) can be developed by summing forces. Gravity effects will cancel out similar to the damped system, and are not included in this derivation. FS + Fd = -may substituting FS = ky and Fd = cv = c(dy/dt) gives, Recall, solving any differential equation requires that a general solution is first assumed and then initial conditions are used to find the constants. For an undamped system, both sin and cos functions were used in the solution. For the damped system, it is more convenient to use an exponential form as, y(t) = Dest where A is an arbitrary constant, and s is a characteristic parameter. Substituting this into the equation of motion will give (ms2 + cs + k ) Dest = 0 |
||||
For nontrivial solutions (D ≠ 0), the two possible roots, s1 and s2, are
and the general solution is where A and B are constants that are determined from initial or boundary conditions. When the square root term is equal to zero, the two roots are equal which gives critical damping, cc, as |
|||||
To help simplify the equations another constant is used, the damping ratio or damping factor, ζ. This term denotes the severity of the damping. Now, the roots can be simplified to Depending on the term within the radical, the system is said to be overdamped, underdamped or critically damped. ζ = 1 Critically Damped |
|||||
| Critically Damped (ζ = 1) |
|||||
|
|
For ζ = 1, the roots s1 and s2 are equal, s1 = s2 = -ωn The general solution to the differential equation is The coefficients A and B are |
||||
| Overdamped (ζ > 1) (Non-Oscillatory) |
|||||
 Overdamped |
For an overdamped system, general solution is The constants A and B are determined from the initial conditions, |
||||
| Underdamped (ζ < 1) (Oscillatory) |
|||||
|
|
When ζ < 1, underdamped system, the roots are Here, ωd is referred to as the damped frequency, Combining with the general solution gives This can be simplified to give where the constants C and D are |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.