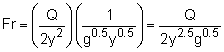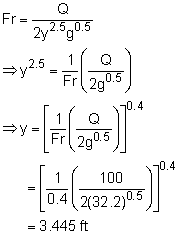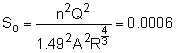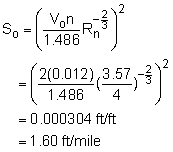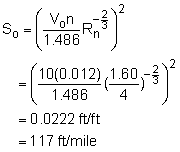| Ch 10. Open-Channel Flow | Multimedia Engineering Fluids | ||||||
|
Uniform Flow |
Gradually Varied Flow |
Rapidly Varied Flow |
|||||
| Uniform Flow | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Question #1 |
||
|
|
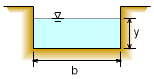
Design a rectangular concrete channel to carry 100 cfs if y/b is 0.5 and it is desired to keep the Froude number less than or equal to 0.4. Assume uniform flow. |
|
| Solution #1 |
||
The Froude number is defined as for rectangular or very wide channels, where y is the water depth. Fr < 1.0: subcritical flow Hence, Fr ≤ 0.4 implies that the flow is subcritical. The velocity is given by The Froude number is then given by Solve for y when Fr = 0.4: |
||
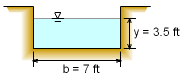 Final Dimensions of the Rectangular Channel |
The width b is then given by b = 2y = 2(3.445 ft) = 6.890 ft In practice, round b to 7.0 ft and y to 3.5 ft. The Froude number is which meets the design requirement. Now, the slope needed to carry this flow can be found from Manning's equation where n = 0.013 for concrete Solve for So |
|
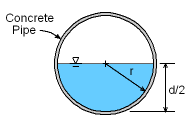 Concrete Pipe |
Question #2 |
|
| Design a concrete pipe (i.e., diameter and permissable slope) to carry the 10-year storm runoff of 10 ft3/s flowing half full. To keep solids suspended, the average velocity must be > 2 ft/s. To prevent scour, the average velocity must be less than 10 ft/s. | ||
| Solution #2 |
||
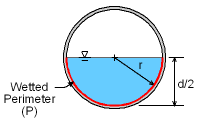 Wetted Perimeter |
Use Manning equation: and Q = VoA Use n = 0.012 for concrete For full pipe: A = π d2 / 4 Rh = A/P where P is the wetted perimeter Given the design requirement that the pipe be half full, there will be one set of values (a diameter and a slope) for any velocity. At the low end, Vo = 2 ft/s |
|
Solve for the corresponding slope using Manning's equation, which
gives tan-1(0.000304) = 0.0174° At the high end, Vo = 10 fps Solve for the corresponding slope: tan-1(0.0222) = 1.27o |
||