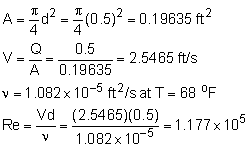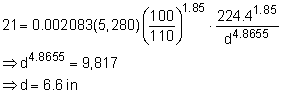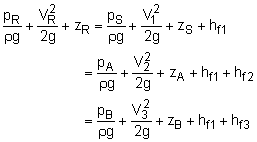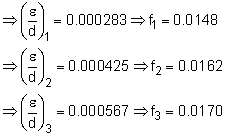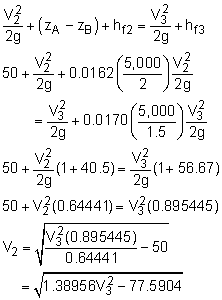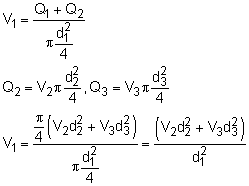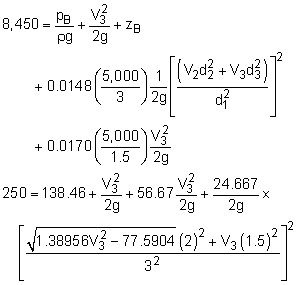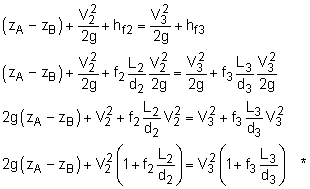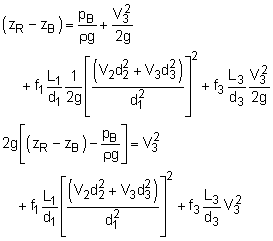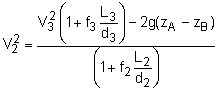Flow between Two Reservoirs

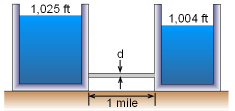
It is desired to limit the flow between two reservoirs by using a small diameter pipe, as shown below. What diameter, d, is required for a discharge rate of 0.5 cfs (use Darcy-Weisbach). How does your answer change if you use Hazen-Williams to compute friction loss?

Darcy-Weisbach equation:

h₁ - h_f = h₂
h_f = h₁ - h₂ = h_e1 + h_p1 + h_v1 - (h_e2 + h_p2 + h_v2)

where
h_e = elevation head = z
h_p = pressure head = p/ρg
h_v = velocity head = V²/2g

Total head does not vary with depth in a reservoir because vertical velocities are negligibly small. Therefore, z + p/ρg = h_e + h_p = C

Since we are calculating head loss due to friction over the length of the pipe, the velocity terms cancel out because V₁ = V₂

This leaves

     h_f = h_e1 + h_p1 - h_e2 - h_p2 = 1,025 - 1,004 = 21 ft

Given Q, calculating d is an iterative process.

1^st: Guess a reasonable d
Guess d = 0.5 ft

Relative roughness = ε/d

For commercial, new pipe: ε = 0.00015 ft

From Moody chart, f = 0.0195

Solve Darcy-Weisbach equation for d:

Use d = 0.494 ft:

From Moody chart, f = 0.0195

Our solution has converged, hence d = 0.5 ft = 6 in.

Using Hazen-Williams (commonly used in practice) (assume turbulent flow, valid for water at 20 ^oC, constant loss coefficient)

where L in feet, h_f in feet, and d in inches

     1 gal/min = 0.002228 cfs

Use C for smooth steel, C = 110

Note: This is an empirical formula, so units don't cancel. Make sure you know the units necessary for each variable.

Problem Diagram

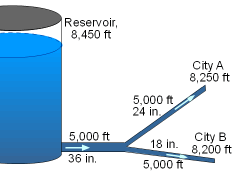
(1) Use the Darcy-Weisbach equation to find the flow delivered to each city (pressure at end is 60 psig)
(2) How much would the pipe to B have to be increased to increase the flow by 10%?
(3) For conditions of part (1), estimate the population of each city.

(1)
    
where
z_R = 8,450 ft
z_A = 8,250 ft
z_B = 8,200 ft

L₁ = L₂ = L₃ = 5,000 ft
d₁ = 3 ft, d₂ = 2 ft, d₃ = 1.5 ft
ε = 0.00085 ft

Assume Re = 2 x 10⁶ (flat portion of Moody chart)

Equating (A) and (B) (p_A = p_B = 60 psig, as given)

Equating (R) and (B):

Solve for V₃: V₃ = 10.36 ft/s, and V₂ = 8.459 ft/s

Check Moody chart: f₁ = 0.0155, f₂ = 0.0162, and
f₃ = 0.0172, hence the estimates were pretty good.

Could use new values of f and make sure it converges, but for this example, solution. I won't.

     Q_A = V₂(π/4)d₂² = 26.57 cfs
     Q_B = V₃(π/4)d₃² = 18.31 cfs

(3) 165 gallons per person per day (consumption in U. S., approximate, USGS data)

1 gpm = 0.002228 ft³/s

Q_A = 1.717 E⁷ gallons per day
Q_B = 1.1834 E⁷ gallons per day

Population A = 1.717 E⁷/165 = 104,000 people
Population B = 1.1834 E⁷/165 = 71,700 people

(2) The equations are the same to start with but
Q₃ = (18.31)(1.1) = 20.14 cfs

You cannot assume the head loss in the pipes is the same, since the added flow to city B will have an effect on the flow through pipes 1 and 2 as well. Therefore, the new variables are d₃ and V₂. Since Q₃ is known, V₃ and d₃ are related. Therefore, only one independent variable.

This problem is more difficult than part (1) because f₃ depends on ε/d₃, so it becomes an iterative problem.

Equating (A) and (B):

Equating (R) and (B):

Solve and substitute in V₂ from * above and solve equations, iterating for d.

Guess d to start, find ε/d, V, calculate a Re and obtain f₃ from Moody chart, and solve for d.

Repeat until convergence.

Guess d = 18 in. (same as part (1))
ε/d = 0.000567
f₃ = 0.0170

     
V₂ = 10.14 ft/s
d₃ = 1.56 ft
ε/d = 0.000544

Based on previous velocities and new dimensions of d and new Re's:

f₁ = 0.0155
f₂ = 0.0165
f₃ = 0.0171

V₂ = 8.335 ft/s
d₃ = 1.565 ft

Convergence, hence d₃ = 18.8 inches

Note: changing the flow to city B changes the flow to city A, even though the pipe to A wasn't changed.

The net flow rate = (π/4)(2 ft)²(8.24 ft/s) = 25.89 cfs
Q_A = (25.89)(646,320) = 1.673E⁷ gallons/day

Therefore, there was a decrease of 440,000 gallons/day to city A, which is the water used by (440,000)/165 = 2,670 people.

It is important to understand the consequences of design modifications. To maintain the same flow to city A while increasing flow to city B, the pipe to city A also needs to be larger, to some degree.