| Ch 4. The Mean Value Theorem | Multimedia Engineering Math | ||||||
|
Maximum & Minimum |
Rolle's Theorem |
Mean Value Theorem |
Monotonic Functions |
First Derivative Test |
Concavity & Inflection |
Second Derivative Test |
|
| First Derivative Test | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| MATHEMATICS - THEORY |
||
| The First Derivative Test |
||
| Recall that Fermat's Theorem states that if a function has a local extreme value at a point, then that point is a critical point of the function. However, a critical point does not guarantee an extreme value. Thus, a test is needed to determine whether a local extreme value is located at a critical point or not. It is called the first derivative test. It states: | ||
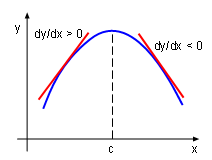 Local Maximum
|
Suppose x0, is a critical point of a continuous function.
The concept of the first derivative test can be better understand by explaining the following example. Examining the case when the derivative of a function changes from positive to negative as shown on the left graphic. When x < c, the derivative of the function is positive, according to the Test for Monotonic Functions the function is increasing. That is f(c) > f(x) when x < c. When x > c, the derivative of the function is negative, according to the Test for Monotonic Functions the function is decreasing. That is f(c) > f(x) when x > c. Thus, f(c) is the local maximum according to the local maximum definition.
|
|
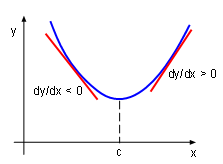 Local Minimum
Local Minimum