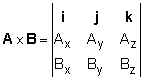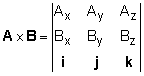| Ch 4. Moments/Equivalent Systems | Multimedia Engineering Statics | ||||||
|
Moment 2-D Scalar |
Moment 3-D Scalar |
Moment 3-D Vector |
Couples and Equiv. System | Distributed Loads, Intro | |||
| Moment of Force: 3-D Vector | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| The Cross Product |
||
|
|
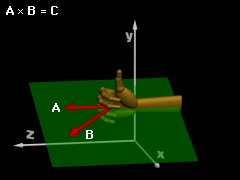
The dot product was previously introduced as a way of "multiplying" vectors where the result is a scalar, A • B = AB cosθ The second method for "multiplying" vectors is called the cross product, and the result is a vector. The cross product of two vectors A and B gives the vector C that has a magnitude of |C| = |A × B| = AB sinθ Here θ is the angle between the vectors A and B. The vector C is perpendicular to the plane defined by the vectors A and B, and the direction is determined from the right-hand rule. |
|
| Cross Product with Cartesian Vectors |
||
|
If the vectors A and B are in Cartesian form, then it can be shown that the cross product of A and B is given by the determinant of the unit vectors and the Cartesian components of A and B. It is interesting to note that this determinant could also be written as, The results will be the same for either form. |
||
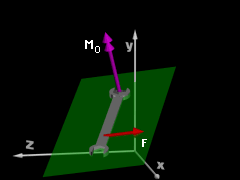
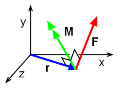 Vectors r and F are always perpendicular to M ( = r × F)
|
Moment as a Cross Product |
|
|
If the moment of a force F about the point O is represented by the vector Mo, then it can be shown that Mo = r × F Here r is the position vector of any point on the line of action of F with respect to point O. Expanding the determinant form of the cross product, gives Mo = (ry Fz
- rz Fy)i + (rz Fx
- rx Fz)j From this equation, the Cartesian components of the moment vector Mo
are readily found. |
||
| Moment of a Force About a Line or Axis |
||
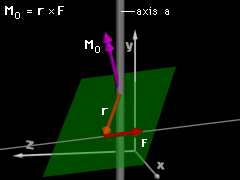 Moment About an Axis |
In many problems, it is necessary to determine the moment of a force about a certain line or axis, such as an axle on a car. Since the moment of a force is a vector, the dot product can be used to determine its component parallel to any line a. Ma = (Mo
• ua) ua Here ua is the unit vector in either direction of the line a. |
|