| Ch 4. Moments/Equivalent Systems | Multimedia Engineering Statics | ||||||
|
Moment 2-D Scalar |
Moment 3-D Scalar |
Moment 3-D Vector |
Couples and Equiv. System | Distributed Loads, Intro | |||
| Moment of Force: 3-D Scalar | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
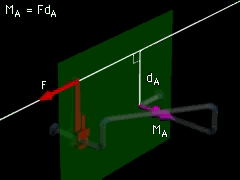 Joint A |
Joint A |
|
|
The line of action of the force is 30 cm from joint A. Therefore, the
magnitude of the bending moment is = (80 N) (30 cm) = 2,400 N-cm |
||
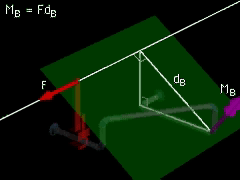 Joint B |
Joint B |
|
|
The distance from joint B to the line of action of F is found from the Pythagorean theorem: dB = (302 + 452)0.5 = 54.08 cm Substitute and solve for the magnitude of the moment: MB = (80 N) (54.08 cm) = 4,327 N-cm
|
||
 Joint C |
Joint C |
|
|
Calculate the moment arm and the moment at joint C in the same manner as for joint B: dC = (152 + 452)0.5 = 47.43 cm MC = (80 N) (47.43 cm) = 3,795 N-cm
|
||
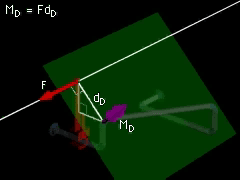 Joint D |
Joint D and E |
|
|
Calculate the moment of F at joints D and E in the same manner as for joints B and C: dD = (152 + 152)0.5 = 21.21 cm MD = (80 N) (21.21 cm) = 1,697 N-cm dE = (302 + 152)0.5 = 33.54 cm ME = (80 N) (33.54 cm) = 2,683 N-cm
|
||
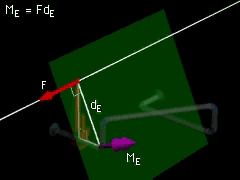 Joint E |
Maximum Moment |
|
|
The joint with the largest moment is joint B, which has a moment of 4,327 N cm, or in more common units 43.27 N-m.
|
||