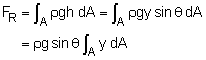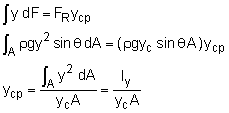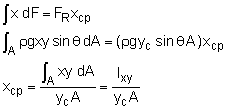| Ch 2. Fluid Statics | Multimedia Engineering Fluids | ||||||
|
Pressure Variation |
Pressure Measurement |
Hydrostatic Force(Plane) |
Hydrostatic Force(Curved) |
Buoyancy | |||
| Hydrostatic Force - Plane Surface | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||
| In this section, the discussion is focused on how to determine hydrostatic forces exerted on a plane surface submerged in a static fluid. Determining this hydrostatic force is particularly crucial in the design of engineering structures, such as dams, storage tanks and hydraulic systems. The concept of using a pressure prism to obtain the hydrostatic force will also be introduced. | |||||
| Hydrostatic Force on a Plane Surface |
|||||
|
|
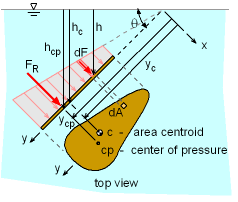
Consider an inclined plane submerged in a static fluid as shown in the figure. The resultant force FR is acting perpendicular to the plane since no shear force is present when the fluid is at rest. FR has a line of action that passes through the point (xcp , ycp), which is called the center of pressure. Note that the pressure acting perpendicular to the plane surface is also referred to as the normal stress. Now take a small differential element dA at a depth of h. The differential
force dF acting on dA is given by |
||||
The integral where yc is the y coordinate of the centroid of the plane surface. From trigonometry, where hc is the vertical distance from the fluid surface to the centroid of the plane surface. The resultant force is simplified to |
|||||
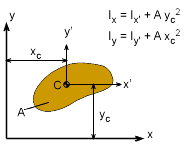 Parallel Axis Theorem |
The center of pressure, xcp and ycp can be obtained by summing moments about the y and x axis, respectively. First, by equating the sum of moments of all pressure forces about the x axis to the moment of the resultant force: where Ix = Ix' + Ayc2
|
||||
Similarly, xcp can be obtained by equating the sum of moments of all pressure forces about the y axis to the moment of the resultant force where
The values for the second moment of inertia and product of inertia with respect to the centroidal axes for various common geometries are given in the appendix. From the formulations of xcp and ycp, it is noted that the center of pressure is always lower in the liquid than the centroid of the plane area. |
|||||
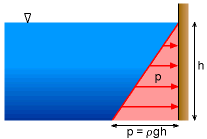
| Pressure Prism |
|||||
|
|
An alternate approach of determining the hydrostatic force is by means of a pressure prism. Consider a vertical plane submerged in a static fluid, as shown in the figure. The pressure increases linearly with the depth. One can then easily construct a corresponding three-dimensional diagram of the pressure distribution, and such a volume is called a pressure prism. The resultant force is the total volume of the pressure prism, that is FR = Volume = 1/2 (ρgh) (bh) The resultant force passes through the centroid of the pressure prism. For this particular example, the centroid of a triangular element is located at a distance of h/3 from its base and lies in the vertical symmetry axis. As illustrated, this method is particularly convenient when the shape of the pressure prism is a common geometry, in which the volume and centroid can be readily obtained. |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.